Wie Bestimmt Man Den Summenwert Der Geometrischen Reihe?
Di: Ava
Im Mathe-Forum OnlineMathe.de wurden schon tausende Fragen zur Mathematik beantwortet. So auch zum Thema Summenwert Wir haben oben und im Kapitel zuvor schon gesehen, dass die geometrische Reihe den Konvergenzradius hat. Ebenso haben die mit der geometrischen Reihe verwandten Reihen und den Konvergenzradius , denn ist , so gilt für alle . Daher konvergiert die Reihe Majorantenkriterium mit der geometrischen Reihe als Majorante.
Geometrische Reihe • einfach erklärt
Eine Reihe ist der Grenzwert der Partialsummen einer Folge. Das klingt kompliziert! Verständlicher: Eine Reihe ist die Aufsummierung aller Folgenglieder.
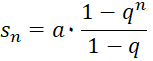
Das ist eine geometrischen Reihe, bei der der Bezug zu e völlig unnötig ist. Mache noch eine Indexverschiebung von k=3 zu k=0, dafür wird aus dem Exponenten k-2 der Exponent k+1.
Mit der geometrischen Summenformel kannst du Summen mit einem Exponenten schnell ausrechnen. Dabei kannst du für q jede reelle Zahl einsetzen, außer die 1. Das n steht wie meistens für eine natürliche Zahl. Häufig brauchst du die geometrische Summenformel, um die Partialsumme einer geometrischen Reihe auszurechnen.
Für eine konvergente Reihe (mit einem endlichen Summenwert) müssten beide Teilreihen separat konvergent sein. Da es sich um einfache geometrische Reihen handelt, ist hier auch leicht abzusehen, für welche Werte von x dies der Fall ist: In einem Lehrbuch der Mathematik von 1940 (1) findet man, wie in fast allen Lehrbüchern, die geometrische Folgen behandeln, die berühmte Weizen-Schachbrett-Aufgabe. Holen Sie sich umfassende Hausaufgabenhilfe für Geometrische Folge! Durchsuchen Sie die Fragen, die Schüler auf Geometrische Folge gestellt haben und sehen Sie, wie Flexi ihnen mit Antworten und klaren Erklärungen geholfen hat.
Es versteht sich nach Gleichung (5), dass sich die geometrische Reihe auch konstruieren lässt, indem das erste Glied mit q multipliziert wird, das zweite Glied mit q und so weiter. So gesehen kann man q auch als konstituierenden Faktor der geometrischen Reihe bezeichnen.
Ich weiß, dass eine geometrische Reihe wie folgt definiert ist. ∑ k = 0 ∞ a 0 ⋅ q k = a 0 1 – q Ich würde nun wie folgt umformen Summenwert einer Reihe berechnen im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen! Geometrische Reihe Die geometrische Reihe ∑ n = 0 ∞ x n n=0∑∞ xn konvergiert absolut für ∣ x ∣ <1 ∣x∣ <1 und divergiert für ∣ x ∣ ≥ 1 ∣x∣ ≥ 1.
Der Reihen-Rechner berechnet die Summe einer Reihe über das vorgegebene Intervall. Er ist in der Lage, Summen von endlichen und unendlichen Folgen zu berechnen. habe ein kleines Problem mit folgenden Aufgaben: 1) Zu ermitteln ist, ob die Reihe konvergiert und der Reihenwert; ∑ n = 2 ∞ 2 n + 2 3 n \sum _ { n=2 }^ { \infty } { \frac { { 2 }^ { n+2 } } { { 3 }^ { n } } } n=2∑∞ 3n2n+2 nach dem Quotientenkriterium konvergiert sie. Bzgl. des Reihenwertes haben wir den Tipp bekommen, dass man die geometrische Reihe anwenden könnte Als Im Mathe-Forum OnlineMathe.de wurden schon tausende Fragen zur Mathematik beantwortet. So auch zum Thema Geometrische Reihe, Überprüfen und Reihenwert
ich muss den Summenwert einer unendlichen Reihe bestimmen und weiß aber nicht richtig wie ich da vorgehen aber nicht mehr weiter. für eure Hilfe! Veranschaulichung der geometrischen Reihe Die geometrische Reihe zum Parameter q versucht, alle Potenzen q 0 = 1, q 1 = q, q 2, q 3, q 4
Der geometrische-Folge-Rechner findet den n-ten-Wert und die Summe einer geometrischen Folge (soweit möglich bis ins Unendliche).

Zur Vereinfachung wird der Entwicklungspunkt in den Ursprung verschoben (). Nun wählt man, wie in der Abbildung skizziert, zwei Kreise, die den Punkt einschließen. Dann gilt nach der Cauchyschen Integralformel wobei das Minuszeichen die Orientierung von umkehrt; ist der orientierte Rand eines Kreisrings, der enthält.
Aufgabe: Sei 0 Beim zweiten Gleichheitszeichen verwenden wir die Formel für die geometrische Summe und beim dritten den Grenzwert (+). Wir besprechen unendliche Summen später genauer, für jetzt genügt erneut ein intuitiver Grenzwertbegriff. Addiert man alle Glieder einer geometrischen Folge, also eine Folge von Zahlen, die sich untereinander stets um den gleichen Faktor unterscheiden, so ergibt sich eine geometrische Reihe. Im Mathe-Forum OnlineMathe.de wurden schon tausende Fragen zur Mathematik beantwortet. So auch zum Thema Umformungen der geometrischen Reihe Die Geometrische Reihe wird aus den Gliedern der Nullfolge q n = 1 p n qn = pn1 gebildet. Hat diese Reihe einen endlichen Grenzwert? Die Summe der geometrischen Reihe ist bekannt: s n = q 0 + q 1 + q 2 + q 3 + q 4 + = q n + 1 1 q 1 sn = q0 +q1+q2+q3 +q4 +..= q−1qn+1−1 Gl. 178 Für p> 1 p> 1 ist q <1 q <1, daher S = lim n → ∞ s n = lim n → ∞ 1 q n 1 q = 1 1 q w e g e n lim n → Rektifizierbarkeit widerlegen Universität / Fachhochschule Differentiation Folgen und Reihen Grenzwerte Partielle Differentialgleichungen Tags: Differentiation, Folgen und Reihen, Grenzwert, Partielle Differentialgleichungen Zunächst betrachten wir den Spezialfall , also die Binomilareihe : Berechnet man man die Koeffizienten , so erhält man wie folgt einen Spezialfall der geometrische Reihe: Im Mathe-Forum OnlineMathe.de wurden schon tausende Fragen zur Mathematik beantwortet. So auch zum Thema Summenwert bestimmen Bei einer geometrischen Reihe ist der Quotient q zweier benachbarter Folgeglieder konstant. Das a steht einfach für irgendeinen Rest, der konstant ist, also beispielsweise eine Zahl wie 1. Die geometrische Reihe hat die Form . Sie ist eine wichtige Reihe, die dir häufig in Beweisen und Herleitungen begegnen wird. Außerdem kann man mit der geometrischen Reihe Konvergenzkritierien wie das Quotientenoder das Wurzelkriterium beweisen. Wert einer Reihe berechnen Universität / Fachhochschule Folgen und Reihen Tags: Folgen und Reihen, reih, Wert Arithmetische Reihe Definition Eine arithmetische Reihe summiert die Glieder einer arithmetischen Folge (also einer Folge, bei welcher der Abstand zwischen den Folgegliedern konstant ist, zum Beispiel 2, 5, 8 und 11 mit jeweils 3 Abstand) auf. Nur in wenigen Fällen ist die explizite Berechnung einer Reihe möglich. Ein Beispiel sind bestimmte Reihen mit rationalen Summanden wie Nach der Partialbruchzerlegung lässt sich diese Reihe in der Form schreiben. Bis auf und heben sich alle Summanden auf, so dass der Grenzwert unmittelbar abgelesen werden kann. 8.5. Geometrische Reihe Werden die Glieder einer geometrischen folge addiert, so spricht man von einer geometrischen Reihe. Die Summe der geometrischen Reihe berechnet man mit folgender Summenformel s n = a 1 q n 1 q 1, q ≠ 1 sn = a1 ⋅ q−1qn−1,q = 1 Im zweiten Teil soll ich den Summenwert ermitteln (bis 99)! Hier weiß ich leider nicht, wie ich vorgehen soll. Mir ist nur eine Summenformel für arithmentische und geometrische Reihen bekannt, allerdings nicht für harmonische Reihen! Bin um jede Hilfe dankbar Grüße, Flasher 15.11.2006, 13:50 klarsoweit Auf diesen Beitrag In diesem Video wird dir erklärt, was eine geometrische Reihe ist. Du lernst, wie du die Summe unendlich vieler Zahlen berechnest und wie du die Formel dafür anwendest. Am Ende wirst du verstehen, wie geometrische Reihen in der Mathematik verwendet werden. Reihe: Behauptung 0.9999 = 1 Universität / Fachhochschule Folgen und Reihen Grenzwerte Tags: Folgen, Grenzwert, Reihen Einführendes Beispiel: Setzt man in der Summenformel der nichtabbrechenden geometrischen Reihe a1 =1 und q = x so erhält man die Potenzreihe. Eine geometrische Zahlenfolge ist dadurch charakterisiert, dass die Folgenglieder jeweils durch Multiplikation mit dem konstanten Faktor q aus dem vorhergehenden Glied entstehen.Jedes Folgenglied (außer dem ersten) ist das geometrische Mittel seiner beiden Nachbarglieder.