QQCWB

GV

Ulam’S Packing Conjecture _ The 3-ball is a local pessimum for packing

Di: Ava

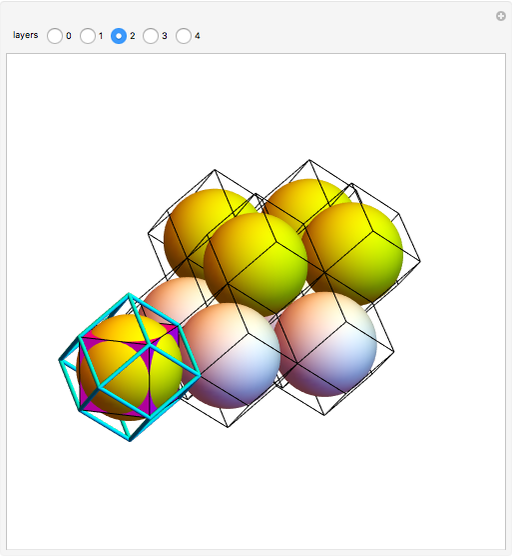
On Ulam’s packing conjecture: is the ball the worst shape for packing? YOAV KALLUS, Princeton University — The question of which convex shapes leave the most empty space in their densest packing is the subject of Rein-hardt’s conjecture in two dimensions and Ulam’s conjecture in three dimensions. In two dimensions, a regular octagon whose corners have been smoothed to arcs If the Erdős–Ulam problem has a positive solution, it would provide a counterexample to the Bombieri–Lang [4][5] conjecture and to the abc conjecture. [6] It would also solve Harborth’s conjecture, on the existence of drawings of planar graphs in which all distances are integers. If a dense rational-distance set exists, any straight-line drawing of a planar graph could be Also see : Ulam’s packing conjecture plugin-autotooltip__plain plugin-autotooltip_bigUlam’s packing conjecture When packing convex identical 3-dimensional objects into a defined space, is a sphere the most ‚efficient‘ shape when considering the amount of free space in the gaps? According to the conjecture, the sphere is the convex solid which forces the largest fraction of

Pessimal Shapes for Packing

Figure 1 from The tree packing conjecture for trees of almost linear ...

Ulam’s packing conjecture, named for Stanislaw Ulam, is a conjecture about the highest possible packing density of identical convex solids in three-dimensional Euclidean space. The result is consistent with the Ulam’s packing conjecture 38 that the optimal packing density for congruent sphere packings is smaller than that for any other convex body. Stanislaw Ulam 의 이름을 따서 명명된 Ulam 의 패킹 추측은 3차원 유클리드 공간에서 동일 한 볼록 고체 의 가능한 가장 높은 패킹 밀도 에 대한 추측입니다. 이 추측은 합동 구를 패킹 하기 위한 최적 의 밀도가 다른 볼록체의 밀도보다 작다는 것을 말합니다.

Ulam’s Last Conjecture Putative optimal packing densities due to P.F. Damasceno, M. Engel, and S.C. Glotzer, 2012. \Stanislaw Ulam told me in 1972 that he suspected the sphere was the worst case of dense packing of identical convex solids, but that this would be di cult to prove.“ (Martin Gardner, 1995 postscript to the column \Packing Ulam’s packing conjecture, named for Stanislaw Ulam, is a conjecture about the highest possible packing density of identical convex solids in three-dimensional Euclidean space. The conjecture says that the optimal density for packing congruent spheres is

Stanisław Marcin Ulam (Polish: [sta’ɲiswaf ‚mart͡ɕin ‚ulam]; 13 April 1909 – 13 May 1984) was a Polish and American mathematician, nuclear physicist and computer scientist. He participated in the Manhattan Project, originated the Teller–Ulam design of thermonuclear weapons, discovered the concept of the cellular automaton, invented the Monte Carlo method of computation, and and Kepler’s conjecture, now a theorem, says that’s their maximum packing density. So, Ulam’s packing conjecture says we can pack Since too many conjectures already bear the name Ulam’s conjecture, it would be appropriate to refer to this one as Ulam’s packing conjecture, or perhaps even as Ulam’s last conjecture, seeing how it too was published posthumously and how the space in Gardner’s postscript evidently could not fit any motivation for Ulam’s suspicion.

\Stanislaw Ulam told me in 1972 that he suspected the sphere was the worst case of dense packing of identical convex solids, but that this would be di cult to prove.“ Related conjecture: any centrally-symmetric convex shape can be packed using only translations at a higher density than spheres. 1995 postscript to the column \Packing Spheres“ The conjectures in following list were not necessarily generally accepted as true before being disproved. Atiyah conjecture (not a conjecture to start with) Borsuk’s conjecture Chinese hypothesis (not a conjecture to start with) Doomsday conjecture Euler’s sum of powers conjecture Ganea conjecture Generalized Smith conjecture Hauptvermutung Hedetniemi’s conjecture, Here is a short takeout on Ulam’s Conjecture: On the Wikipedia page it say it has been proven up to n=11. Now the Question: If I have to check for the Isomorphism, does this mean, if I take out an Vertex x in Graph one and then show that for all vertices in Graph two it is impossible to get G-x, then they could not be isomorphic? As long I am have less the 11 edges.

Conjecture The regular heptagon is an absolute minimum of the optimal packing fraction among convex bodies. In d = 2, the heptagon is a local minimum of the optimal packing fraction, assuming the \double lattice“ packing of heptagons is their densest packing. The disk is The question of which convex shapes leave the most empty space in their densest packing is the subject of Reinhardt’s conjecture in two dimensions and Ulam’s conjecture in three dimensions.

The Kepler conjecture, proposed by Johannes Kepler, asserts that no arrangement of equally sized spheres can exceed the density of cubic or hexagonal close packing, which is approximately 74.05%. Thomas Hales provided a proof in 1998 through extensive computer calculations, and a formal proof was completed in 2014 with the Flyspeck project. The conjecture has historical

The 3-ball is a local pessimum for packing

  • Ulam’s Conjecture, Graph isomorphism, Application
  • Ulam’S Packing Conjecture Words
  • About: Ulam’s packing conjecture

When packing convex identical 3-dimensional objects into a defined space, is a sphere the most ‚efficient‘ shape when considering the amount of free space in the gaps? According to the conjecture, the sphere is the convex solid which forces the largest fraction of The Kepler conjecture, named after the 17th-century mathematician and astronomer Johannes Kepler, is a mathematical theorem about sphere packing in three-dimensional Euclidean space. It states that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic close packing (face-centered cubic) and hexagonal close packing

Illustrating Kepler's Conjecture on Sphere Packing - Wolfram ...

Chen 4 constructed a crystalline structure formed from nonamers with φ = 0.7786, the first to exceed sphere close packing, and showing that tetrahedra obey Ulam’s conjecture.

Formulated by mathematician Stanislaw Ulam, the conjecture posits that the densest packing of spheres (in three-dimensional space) occurs when the spheres are arranged in a face-centered cubic (FCC) lattice structure or equivalently in a hexagonal close packing (HCP) arrangement. Ulam’s packing conjecture, named for Stanislaw Ulam, is a conjecture about the highest possible packing density of identical convex solids in three-dimensional Euclidean space. The conjecture says that the optimal density for packing congruent spheres is Ulam’s packing conjecture, named for Stanislaw Ulam, is a conjecture about the highest possible packing density of identical convex solids in three-dimensional Euclidean space. The conjecture says that the optimal density for packing congruent spheres is smaller than that for any other convex body. That is, according to the conjecture, the ball is the convex solid which forces the

Pages in category „Unsolved problems in geometry“ The following 48 pages are in this category, out of 48 total. This list may not reflect recent changes.

y not necessarily achieved by any particular body. In three dimensions, the claim that the ball is the minimum of δ(K) has come to be known as Ulam’s packing conjecture, due to a remark Gardner attributes to Ulam, though there is no ev-idence to co

Ulamova pretpostavka o pakiranju , nazvana po Stanislaw Ulam , pretpostavka je o najvećoj mogućoj gustoći pakiranja identičnih konveksnih čvrstih tijela u trodimenzionalnom euklidskom prostoru . Pretpostavka kaže da je optimalna gustoća za pakiranje sukladnih sfera manja od one za bilo koje drugo konveksno tijelo. Ulam’s packing conjecture, named for Stanisław Ulam, is a conjecture about the highest possible packing density of identical convex solids in three-dimensional Euclidean space. The conjecture says that the optimal density for packing congruent spheres is Ulam‘ s packing conjecture is a hypothesis in the field of geometry and combinatorial mathematics, particularly concerning the arrangement of spheres in space. Formulated by mathematician Stanislaw Ulam, the conjecture posits that the densest packing of spheres (in three-dimensional space) occurs when the spheres are arranged in a face-centered cubic

A numerical search for the worst-packing shapes

Ulam’s Last Conjecture \Stanislaw Ulam told me in 1972 that he suspected the sphere was the worst case of dense packing of identical convex solids, but that this would be di cult to prove.“ ˚(B) = ˇ= p 18 = 0:7405 Naive motivation: sphere is the least free solid (three degrees of freedom vs. six for most solids).

Abstract The question of which convex shapes leave the most empty space in their densest packing is the subject of Reinhardt’s conjecture in two dimensions and Ulam’s conjecture in three dimensions.

In this paper, we study the Reconstruction Conjecture for finite simple graphs. Let Γ and Γ′ be finite simple graphs with at least three vertices such han circles [7]. Ulam’s conjecture implies that this would not be the case in three dimensions. Th question then is in which dimensions the ball is a local minimum of the optimal packing density. In this article, we answer t