QQCWB

GV

Relaxed-Inertial Proximal Point Algorithms For Nonconvex

Di: Ava

The proximal point algorithm (PPA) for the convex minimization problem min x ∈ H f (x), where f: H → R ∪ {∞} is a proper, lower semicontinuous (lsc) function in a Hilbert space H is considered. Under this minimal assumption on f, it is proved that the PPA, with positive parameters {λ k} k = 1 ∞, converges in general if and only if σ n = ∑ k = 1 n λ k → ∞. Global convergence Combined with the Prox-SVRG method, an inertial accelerated proximal stochastic variance reduction gradient (IAPSVRG) algorithm was proposed to solve a general nonconvex nonsmooth optimization problem. We propose a relaxed-inertial proximal point type algorithm for solving optimization problems consisting in minimizing strongly quasiconvex func-tions whose variables lie in finitely dimensional linear subspaces, that can be extended to equilibrium problems involving such functions. We also discuss possible modifications of the hypotheses in order to deal with quasiconvex functions.

Abstract: Abstract We propose a relaxed-inertial proximal point algorithm for solving equilibrium problems involving bifunctions which satisfy in the second variable a generalized convexity notion called strong quasiconvexity, introduced by Polyak (Sov Math Dokl 7:72–75, 1966). In this paper, an inertial proximal partially symmetric ADMM is proposed for solving linearly constrained multi-block nonconvex separable optimization, which can improve the computational efficiency by considering the ideas of inertial We propose a relaxed-inertial proximal point algorithm for solving equilibrium problems involving bifunctions which satisfy in the second variable a generalized convexity notion called strong quasiconvexity, introduced by Polyak (Sov Math Dokl 7:72–75, 1966). The method is suitable for solving mixed variational inequalities and inverse mixed variational inequalities

Table 3 from Two-step inertial Bregman proximal alternating linearized ...

However, research on the convergence of the ADMM algorithm which the objective function includes coupled term is still at an early stage. In this paper, we propose an algorithm that combines the two-step inertial technique, Bregman distance, and symmetric ADMM to address nonconvex and nonsmooth nonseparable optimization problems. In this paper, we propose two generalized proximal point algorithms with correction terms and backward inertial extrapolation to find a zero of a maximal monotone operator in Hilbert spaces. Weak convergence results are obtained and a non-asymptotic $ \\mathcal{O}(1/n) $ convergence rate is given. We also give a linear rate of convergence under some standard assumption. We perform some numerical examples to show performances of relaxed inertial proximal-gradient method (54) and relaxed inertial nonconvex proximal gradient algorithm (56).

New Proximal Point Algorithms for Convex Minimization

August 22, 2022 Abstract We propose a relaxed-inertial proximal point type algorithm for solving optimization problems consisting in minimizing strongly quasicon- vex functions whose variables lie in nitely dimensional linear subspaces. A relaxed version of the method where the constraint set is only closed and convex is also discussed, and so is the case of a quasiconvex objective We propose a relaxed-inertial proximal point algorithm for solving equilibrium problems involving bifunctions which satisfy in the second variable a generalized convexity notion called strong quasiconvexity, introduced by Polyak in 1966. The method is suitable for solving mixed variational inequalities and inverse mixed variational inequalities involving strongly quasiconvex functions, In this paper, we study the proximal point algorithm with inertial extrapolation to approximate a solution to the quasi-convex pseudo-monotone equilibrium problem. In the proposed algorithm, the inertial parameter is allowed to take both negative and positive values during implementations. The possibility of the choice of negative values for the inertial

However, research on the convergence of the ADMM algorithm which the objective function includes coupled term is still at an early stage. In this paper, we propose an algorithm that combines the two-step inertial technique, Bregman distance, and symmetric ADMM to address nonconvex and nonsmooth nonseparable optimization problems. In this paper, an inertial proximal partially symmetric ADMM is proposed for solving linearly constrained multi-block nonconvex separable optimization, which can improve the computational efficiency by considering the ideas of inertial

Various proximal point-type algorithms have been explored for solving equilib-rium problems in the convex context. Some of these algorithms employ a bifunction endowed with a generalized monotonicity property rather than the classical mono-tonicity. However, there are only a few recent works that focus on iterative methods for solving equilibrium problems with the We introduce an enhanced inertial proximal minimization algorithm tailored for a category of structured nonconvex and nonsmooth optimization problems. The objective function in question is an aggregation of a smooth function with an associated linear operator, a nonsmooth function dependent on an independent variable, and a mixed function involving two variables.

In this work, we first introduce a two-step inertial proximal Bregman ADMM with dual relaxation approach for solving a group of nonsmooth three-block linear constrained optimization problems in the absence of convexity. The introduced algorithm incorporates two-step inertial effect to each subproblem and integrates two relaxed terms to dual update. A

Abstract We propose a relaxed-inertial proximal point algorithm for sol- ving equilibrium problems involving bifunctions which satisfy in the se- cond variable a generalized convexity notion called strong quasiconvexity, introduced by Polyak in 1966. The method is suitable for solving mixed variational inequalities and inverse mixed variational inequalities involving strongly

(PDF) Smoothing Randomized Block-coordinate Proximal Gradient ...

Abstract We propose a relaxed-inertial proximal point type algorithm for solving optimization problems consisting in minimizing strongly quasicon-vex functions whose variables lie in nitely dimensional linear subspaces. A relaxed version of the method where the constraint set is only closed and convex is also discussed, and so is the case of a quasiconvex objective function. Abstract This paper proposes an Inertial Relaxed Prox-imal Linearized Alternating Direction Method of Multipliers (IRPL-ADMM) for solving gen-eral multi-block nonconvex composite optimiza-tion problems. Distinguishing itself from existing ADMM-style algorithms, our approach imposes a less stringent condition, specifically requiring continuity in only one block of the We show that the classical proximal point algorithm remains convergent when the convexity of the proper lower semicontinuous function to be minimized is relaxed to prox-convexity.

Strongly Quasiconvex Functions: What We Know

A stochastic two-step inertial bregman proximal alternating linearized minimization algorithm for nonconvex and nonsmooth problems, Numer. Algorithms (2023) 1–50. In this paper we study an algorithm for solving a minimization problem composed of a differentiable (possibly nonconvex) and a convex (possibly nondifferentiable) function. The algorithm iPiano combines forward-backward splitting with an inertial force. It can be seen as a nonsmooth split version of the Heavy-ball method from Polyak. A rigorous analysis of the We show that the classical proximal point algorithm remains convergent when the convexity of the proper lower semicontinuous function to be minimized is relaxed to prox-convexity. Keywords: Nonsmooth optimization, Nonconvex optimization, Proximity operator, Proximal point algorithm, Generalized convex function

We propose a relaxed-inertial proximal point type algorithm for solving optimization problems consisting in minimizing strongly quasicon-vex functions whose variables lie in finitely dimensional Abstract This paper proposes a two-point inertial proximal point algorithm to find zero of maximal monotone operators in Hilbert spaces. We obtain weak convergence results and non-asymptotic O (1 / n) convergence rate of our proposed algorithm in non-ergodic sense. Applications of our results to various well-known convex optimization methods, such as the

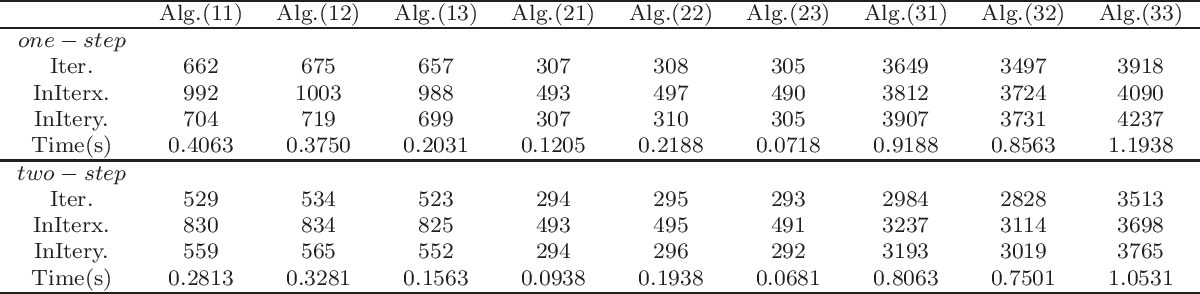
In this paper we showed that forward-backward-forward spliting method with inertial extrapolation can be adapted to solve non-convex mixed variational inequalities. Global convergence results of the sequence of iterates generated by the proposed method is given and some numerical illustrations are also given. It can be easily seen from the graphs that Algorithm (3.1) performs We propose a relaxed-inertial proximal point algorithm for solving equilibrium problems involving bifunctions which satisfy in the second variable a generalized convexity notion called strong quasiconvexity, introduced by Polyak (Sov Math Dokl 7:72–75, 1966). The method is suitable for solving mixed variational inequalities and inverse mixed variational inequalities involving

Abstract We propose a relaxed-inertial proximal point algorithm for sol- ving equilibrium problems involving bifunctions which satisfy in the se- cond variable a generalized convexity notion called strong quasiconvexity, introduced by Polyak in 1966. The method is suitable for solving mixed variational inequalities and inverse mixed variational inequalities involving strongly

A Two-Step Proximal Point Algorithm for Nonconvex Equilibriu

We propose a relaxed-inertial proximal point type algorithm for solving optimization problems consisting in minimizing strongly quasicon-vex functions whose variables lie in finitely dimensional Grad S-M, Lara F, and Marcavillaca RT Relaxed-inertial proximal point algorithms for nonconvex equilibrium problems with applications J. Optim. Theory Appl. 2024 203 2233-2262

Abstract We show that the recent relaxed-inertial proximal point algo-rithm due to Attouch and Cabot remains convergent when the function to be minimized is not convex, being only endowed with certain generalized convexity properties. Numerical experiments showcase the improvements brought by the relaxation and inertia features to the standard proximal point method in this Introduced in the 1970’s by Martinet for minimizing convex functions and extended shortly afterward by Rockafellar towards monotone inclusion problems, the proximal point algorithm turned out to be a viable computational method for solving various classes of optimization problems, in particular with nonconvex objective functions. We propose first a relaxed-inertial • Propose an accelerated linearized augmented Lagrangian method (ALALM) with a linear convergence rate for the strongly convex case. • An accelerated linearized proximal point algorithm (ALPPA) is proposed for both convex and strongly convex cases.

We propose a relaxed-inertial proximal point type algorithm for solving optimization problems consisting in minimizing strongly quasicon-vex functions whose variables lie in finitely dimensional