QQCWB

GV

Random Walks In Varying Dimensions

Di: Ava

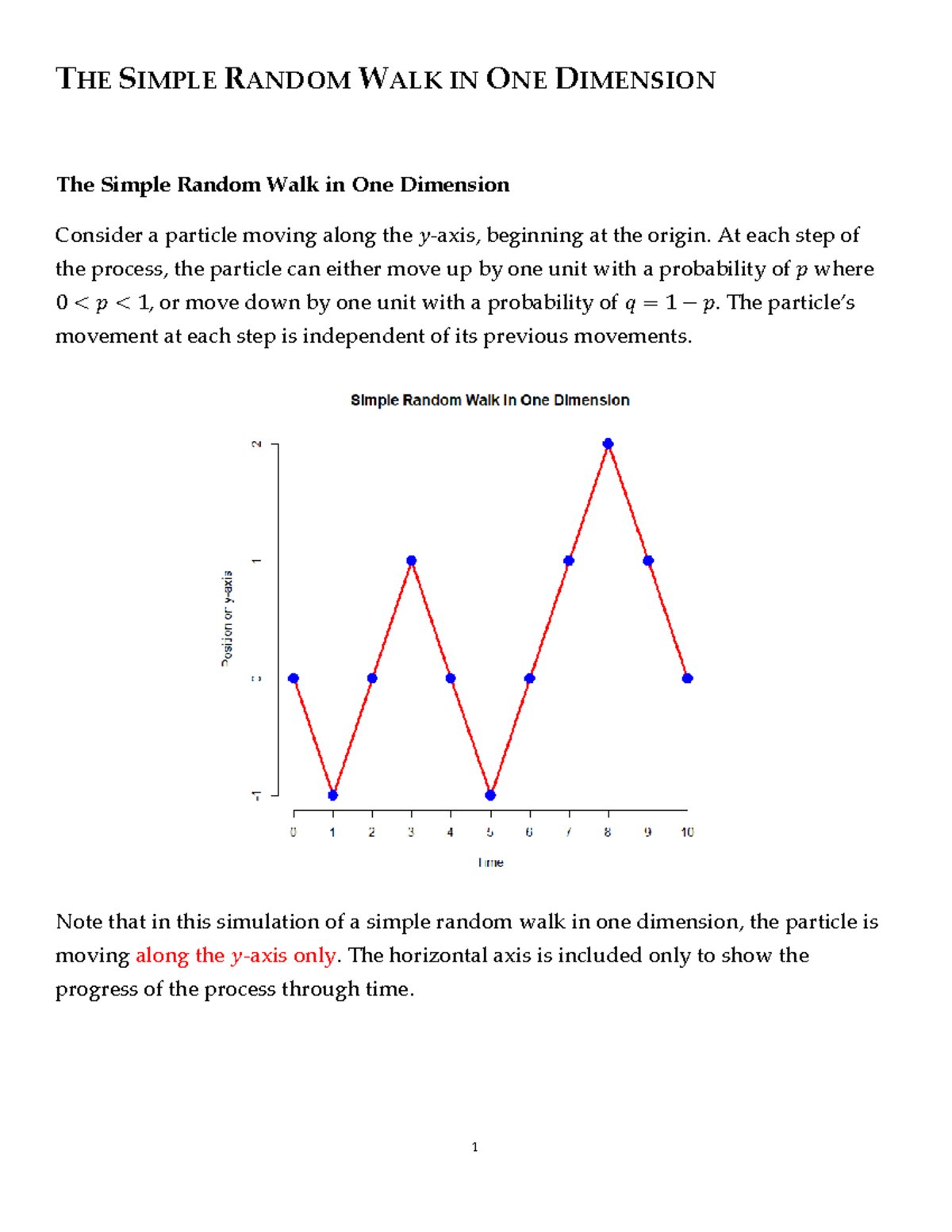
The following sections present some of the more elementary and straightforward applications of random walk and diffusion models in the life and behavioral sciences. Our intention here is to convey basic concepts and to focus on central, original ideas on which these applications are based, not to scrutinize technical details of the examples discussed. The

15-The Simple Random Walk in One Dimension - THE SIMPLE RANDOM WALK IN ...

According to a version of Donsker’s theorem, geodesic random walks on Riemannian manifolds converge to the respective Brownian motion. From a computational perspective, however, evaluating geodesics can be quite costly. We therefore introduce approximate geodesic random walks based on the concept of retractions. We show that these

How do we describe the structure of an amorphous polymer? We need a statistical average over the various conformations, able to provide us with as many information as possible è random walk model. A random walk denotes a path of successive steps in which the direction of each step is uncorrelated with, or independent of, previous steps—steps Time-lagged independent component analysis (tICA) is a widely used dimension reduction method for the analysis of molecular dynamics (MD) trajectories and has proven particularly useful for the construction of protein dynamics Markov models. It identifies those “slow” collective degrees of freedom onto which the projections of a given trajectory show Wenming Hong and Huaming Wang (2010), Quenched moderate deviations principle for random walk in random environment, Science in China Series A-Mathematics, Vol. 53 (8): 1947-1956 Wenming Hong and Lin Zhang (2010), Branching structure for the transient (1;R)-random walk in random environment and its applications, Infinite Dimensional Analysis

Martin capacity for Markov chains and random walks in varying dimensions

Abstract According to a version of Donsker’s theorem, geodesic random walks on Riemannian manifolds converge to the respective Brownian motion. From a computational per-spective, however, evaluating geodesics can be quite costly. We therefore introduce approximate geodesic random walks based on the concept of retractions. We show that these approximate walks We study the evolution of a random walker on a conservative dynamic random environment composed of independent particles performing simple symmetric ran-dom walks, generalizing results of [16] to higher dimensions and more general tran-sition kernels without the assumption of uniform ellipticity or nearest-neighbour jumps. Speci cally, we obtain a strong law of large The derivation above assumes that the walk is on a hypercubic lattice. I am not aware any theoretical derivation of the estimated end-to-end distance for freely jointed random walks in an arbitrary dimension.

Mathematical modelling of the movement of animals, micro-organisms and cells is of great relevance in the fields of biology, ecology and medicine. Movement A popular random walk model is that of a random walk on a regular lattice, where at each step the location jumps to another site according to some probability distribution. In a simple random walk, the location can only jump to neighboring sites of the lattice, forming a lattice path. In a simple symmetric random walk on a locally finite lattice, the probabilities of the location jumping to

Function has to be carefully designed so that numbers “look random”. After generating lots of numbers, they should approximate a defined distribution; for instance evenly distributed numbers from 0 to 1. Shouldn’t be able to predict one number from a Today I will introduce some models and will discuss all dimensions. The second two lectures will focus on work in the last twelve years on two-dimensional systems where conformal invariance becomes important. SIMPLE RANDOM WALK At each step the random walker chooses randomly among its 2d nearest neighbors to move to. The One-Dimensional Random Walk Michael Fowler Flip a Coin, Take a Step The one-dimensional random walk is constructed as follows: You walk along a

What does a random walk have to do with real life? Whew! Now that we’re through with all of that math, how can we relate random walks to real life? If your walk is $ (R_n, S_n)$, then your process is indeed a 2D random walk – but it’s sort of a diagonal random walk since each step is taken in one of the four diagonal directions rather than the cardinal directions. This is fine, because you could just rotate the picture by 45 degrees and obtain an ordinary RW on $\mathbb Z^2$.

In a plane, consider a sum of N two-dimensional vectors with random orientations. Use phasor notation, and let the phase of each vector be Download scientific diagram | First two tICA-projections of random walks with varying dimensions d, each with n = 10000. The lag times of the abrupt changes decrease with increasing dimension

We establish scaling limits for the random walk whose state space is the range of a simple random walk on the four-dimensional integer lattice. These concern the asymptotic behaviour of the graph distance from the origin and the spatial location of the random walk in question. The limiting processes are the analogues of those for higher-dimensional versions of Random walks have been studied for many decades on both regular lattices and (especially in the last couple of decades) on networks with a variety of structures. In the present article, we survey the theory and applications of random walks on networks, restricting ourselves to simple cases of single and non-adaptive random walkers. Formally, a random walk is any process that follows a procession of random steps in a mathematical space such as a lattice or graph. The direction and magnitude of these steps can follow varying probabilistic distributions, leading to interesting properties to study. Random walks can be found within diverse areas of mathematics and science, from animal foraging and cell

Venturing beyond the basic one-dimensional random walks, we encounter the fascinating realm of multidimensional and anomalous random walks, which are pivotal in understanding complex systems across various scientific disciplines.

Abstract We study the evolution of a random walker on a conservative dynamic random environ-ment composed of independent particles performing simple symmetric random walks, generalizing results of [16] to higher dimensions and more general transition kernels without the assumption of uniform ellipticity or nearest-neighbour jumps. Specifically, we obtain a strong

Random walks evolving in a random environment constitute fundamental models in the study of random motions in random media. First introduced and analysed on ℤℤ\mathbb{Z}blackboard_Zin an i.i.d. environment by Solomon [23], this model has since been extensively studied in a wealth of natural settings and shown to capture phenomena that fundamentally distinguishes its 3.3 How to simulate random walks In addition to being quite simple conceptually, random walks are also easy to simulate. The fact that the steps \ (\delta_n = X_n – X_ {n-1}\) are independent coin tosses immediately suggests a feasible strategy: simulate \ (T\) independent coin tosses first, and then define each \ (X_n\) as the sum of the first \ (n\) tosses. Before we implement this Random walks are one of the basic objects studied in probability theory. The moti- vation comes from observations of various random motions in physical and biolog- ical sciences. The most well-known example is the erratic motion of pollen grains immersed in a fluid — observed by botanist Robert Brown in 1827 — caused, as we now know, by collisions with rapid molecules. The

A few years ago, Grimmett, Kesten and Zhang proved that for supercritical bond percolation on Z3, simple random walk on the in nite cluster is a.s. transient. We generalize this result to a class of wedges in the wedge W“ = f(x; y; z) 2 Z3 : x 0; as representing a (2 + „)-dimensional lattice. Z3 including, for any “ 2 (0; 1), jzj x“g which can be thought of Our proof builds on recent work of

Random Walks A random walk considers a „walker“ which starts somewhere, and takes steps in a random direction. In some cases the steps can be of random length as well. The random walk can take place in a plane, along a line, or in higher dimensions. The simplest random walk considers a walker that takes steps of length 1 to the left or right along a line. More complicated random We also determine a formula for the resistance dimension of spherically symmetric random trees and prove that it is equal to the fractal dimension. We emphasize the relationship between these dimensions and the type, of being transient or recurrent, of the Klebaner (1982) and Biggins (1990) extended these results to the branching random walk in varying environ-ment (generation dependent). Gao et al. (2014) considered this central limit theorem for the BRW with random environment in time. Recently, Bansaye (2019) extended it to the model of branching Markov chain in random environment.

Stochastic time series are ubiquitous in nature. In particular, random walks with time-varying statistical properties are found in many scientific disciplines. Here we present a superstatistical Chapter 4 Random Walks A walk?“ said Catharine. “One foot in front of the other,” said Newt, “through leaves, over bridges—” Kurt Vonnegut (Long Walk to Forever) Motivation Now that we have a handle on what a stochastic process actually is, let’s explore this crucial class of processes, both analytically and via simulation in R. We can use the key attributes and topics AB – We prove that a planar random walk with bounded increments and mean zero which is conditioned to stay in a cone converges weakly to the corresponding Brownian meander if and only if the tail distribution of the exit time from the cone is regularly varying. This condition is satisfied in many natural examples. LA – eng KW – conditioned random walks; brownian

Abstract In this paper we present random walk based solutions to diffusion in semi-permeable layered media with varying diffusivity. Martin capacity for Markov chains and random walks in varying dimensions. Retrieved from the University Digital Conservancy, https://hdl.handle.net/11299/2559. Content distributed via the University Digital Conservancy may be subject to additional

4 Estimating the Variance o estimate the variance for the range of two dime random walk. Again, we need to de ne a new random variable to calculate the second moment of Rn. 8 >>>< 1 m;n = We present some results for simple symmetric two-dimensional random walk. Our treatment is based on results concerning independent simple symmetric one-dimensional random walks. We present our recent results on two models of branching processes in random environment. The first model is a branching random walk