Normalverteilung Ohne Sigma, My Und Z
Di: Ava
Normalverteilung und Sigma-Regeln Gegeben ist der Graph der Dichtefunktion einer normalverteilten Zufallsgröße mit μ = 30 und σ = 10 . Bestimmen Sie näherungsweise anhand der Grafik ein Intervall, das symmetrisch um μ liegt und die Wahrscheinlichkeit 0,5 hat.
z-Standardisierung n diesem Tutorial beschäftigen wir uns mit der Z-Standardisierung (auch Z-Transformation genannt). Wir erklären, was der Z-Wert ist, wie die Z-Standardisierung funktioniert und was unter einer Standardnormalverteilung zu verstehen ist. Darüber hinaus erläutern wir, was eine Z-Wert-Tabelle ist und wofür sie verwendet wird.
Diese gelten aber nicht für beliebige – und -Werte, sondern nur für die standardisierte Form der Normalverteilung, bei der jeweils und ist (man spricht auch von einer 0-1-Normalverteilung, Standardnormalverteilung oder normierten Normalverteilung). Parameter ± Quantil Varianz n Die einzigen beiden Unterschiede sind, dass statt dem z -Quantil der Normalverteilung nun das der t-Verteilung verwendet wird, und dass nicht mehr die wahre Standardabweichung σ verwendet wird (da sie ja jetzt unbekannt ist), sondern die Stichprobenvarianz s 2, bzw. ihre Wurzel s verwendet wird. Modellieren mit der Normalverteilung Kann man die Daten sinnvoll durch eine Normalverteilung modellieren? Wenn ja, welche Werte würden Sie für μ und σ wählen?
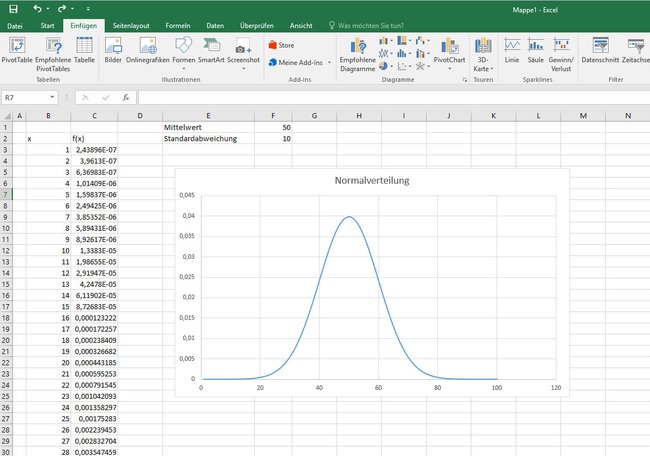
Rechner für Normalverteilung
Konfidenzintervall für den Median Im Fall einer großen Stichprobe mit kann die Verteilung von X und E (X) als asymptotisch normalverteilt angesehen werden. Die Normalverteilung ist symmetrisch. Das bedeutet, dass Erwartungswert und Median zusammenfallen. Das Konfidenzintervall für den Median ist dann identisch mit dem für den Erwartungswert. Letztendlich muss man sich nur ein bisschen an diese Standarisierung und an die Verwendung der Tabelle gewöhnen, dann werden plötzlich alle Rechnungen mit der Normalverteilung einfach. Die Kurve der Normalverteilung wird über eine Funktion beschrieben, die Dichtefunktion der Normalverteilung heißt oder Gauß´sche Glockenkurve. Eine Normalverteilung mit den Parametern und heißt Standardnormalverteilung, standardisierte Normalverteilung[12] oder normierte Normalverteilung[13]. Eine Zufallsvariable, deren Wahrscheinlichkeitsverteilung eine Standardnormalverteilung ist, heißt standardnormalverteilt.
1. Diskrete Verteilungen Diskrete Zufallsgrößen sind Zufallsgrößen, deren Werte endlich oder abzählbar unendlich sind und durchnummeriert werden können. Ihre Wahrscheinlichkeiten kann man in Tabellen oder anschaulich mit Histogrammen darstellen.
Die bekannteste stetige Verteilung ist die Gauß-Verteilung. Sie ist ein Grundmodell für symmetrische Abweichungen von einem Mittelwert und kann in vielen Anwendungen zumindest als Näherung verwendet werden. Sie wird deshalb auch als Sigma-Umgebungen Zusammenhang zwischen Wendepunkt der Wahrscheinlichkeitsfunktion einer Normalverteilung und dem Erwartungswert Der Erwartungswert ist der Wert mit der größten Wahrscheinlichkeit. Links und rechts vom Erwartungswert gruppieren sich die restlichen normalverteilten Wahrscheinlichkeiten. Die Wendepunkte der Wahrscheinlichkeitsfunktion der
- Rechner für die Normalverteilung
- Normalverteilung und Sigma-Regeln
- 4.1 Eigenschaften der Normalverteilung
- Modellieren mit der Normalverteilung
Kapitel7 7 Normalverteilung und t-Verteilung 7.1 Lernziele zu Kapitel 7 – Verteilungsfunktion und Dichtefunktion der Normalverteilung – Standardnormalverteilung – Standardisierung – Quantile der Normalverteilung – Zentraler Grenzwertsatz – Konfidenzintervalle – t-Verteilung 7.2 Verteilungsfunktion und Dichte Eine stetige Zufallsvariable X heißt mit Erwartungswert µ und
Erfahren Sie den Unterschied zwischen Z-Score und T-Score und wann welcher Score verwendet wird. Lernen Sie, wie beide für verschiedene Stichproben und Verteilungen eingesetzt werden, und verstehen Sie deren Rolle in der statistischen Analyse. Die Normalverteilung, auch Gaußsche Glockenkurve genannt, beschreibt, wie viele natürliche Merkmale wie Körpergröße oder Intelligenz in einer Bevölkerung verteilt sind – die meisten Werte liegen um den Mittelwert, extreme Werte sind selten. Sie ist zentral in der Statistik, weil sie Wahrscheinlichkeiten für das Auftreten bestimmter Werte berechenbar macht und viele reale Bias = x̄ – xm Fähigkeitsindizes Cg und Cgk berechnen (optional, mit Einschränkung): Obwohl Cg und Cgk für einseitig unbegrenzte Merkmale ohne natürliche Grenze nicht direkt interpretierbar sind, werden sie im Dokument „Bosch Heft 10“ für Verfahren 1 dennoch berechnet.
Was ist Z-Verteilung? Die Z-Verteilung, auch bekannt als Standardnormalverteilung, ist eine spezielle Art der Normalverteilung, die durch einen Mittelwert von Null und eine Standardabweichung von Eins gekennzeichnet ist. Sie ist ein grundlegendes Konzept in der Statistik und wird in verschiedenen Bereichen häufig verwendet, darunter Datenanalyse, 17. Multivariate Normalverteilung # Vortragsaufzeichnung zur multivariaten Normalverteilung 17.1. Dichten von multivariaten Verteilungen # Wir erinnern uns: Bei einer Dichtefunktion f: R → [0, ∞) für eine Verteilung P einer reellen Zufallsvariable X ist P (X Die Normalverteilung ist ein wichtiges Modell; es ist mathematisch einfach zu handhaben. Der Praktiker muß sich damit abfinden, daß es, streng genommen, in der Empirie keine Normalverteilung gibt. Indessen lassen sich viele mehr oder weniger symmetrisch-eingipflig ver teilte Beobachtungen als angenähert normalverteilt auf fassen und mit dem hierfür Korrelation | Lineare Regression | Varianz und Standardabweichung | Normalverteilung Rechner für die Normalverteilung Berechnungen mit der Formel der Normalverteilung und der Standardnormalverteilung. Bitte Mittelwert und Standardabweichung, sowie einen Eingabewert angeben, um den Funktionswert der Normalverteilung an dieser Stelle zu ermitteln. • Rechner für Normalverteilung Dieses Programm berechnet die Wahrscheinlichkeit, daß eine normalverteilte Zufallsvariable X (mit dem Erwartungswert E (X)= μ und der Standardabweichung σ) im Intervall [x 0;x 1] liegt. Die Normalverteilung wird verwendet, um Häufigkeiten von Daten und Beobachtungen darzustellen. Wir erklären dir, wie du sie interpretierst. Was ist die Normalverteilung überhaupt? Die Normalverteilung beschreibt, wie sich gemessene Werte um einen Durchschnitt herum verteilen. Obwohl auch andere Verteilungsfunktionen genutzt werden, ist diese „Glockenkurve“ die zentrale Grundlage in der modernen Qualitätsstatistik. z Standardisierung einfach erklärt z Transformation Statistik Beispiel z-Wert berechnen & interpretieren mit kostenlosem Video Ausreißertests – Grundregeln Author: Hans Lohninger Basierend auf der Standardabweichung Wenn wir eine Normalverteilung annehmen, kann ein einzelner Wert als Ausreißer betrachtet werden, wenn er außerhalb eines bestimmten Bereichs der Standardabweichung liegt. In vielen Fällen wird ein Faktor von 2,5 verwendet, was besagt, dass ungefähr 99 % der Daten einer Damit du die Sigma-Regeln wirklich verstehst, musst du dir auch ihre Anwendung anschauen. Dazu betrachten wir die Normalverteilung des Intelligenzquotienten in Deutschland. Hier ist der Erwartungswert μ = 100 und die Standardabweichung Sigma σ = 15 gegeben. 1. Diskrete Verteilungen Diskrete Zufallsgrößen sind Zufallsgrößen, deren Werte endlich oder abzählbar unendlich sind und durchnummeriert werden können. Ihre Wahrscheinlichkeiten kann man in Tabellen oder anschaulich mit Histogrammen darstellen. Die Bedingung beruht nicht auf einer mathematischen Herleitung, sondern auf praktische AnwendbarkeitDamit die Binominalverteilung sich Es liegt deshalb die Frage nahe, ob man eine beliebige Normalverteilung in eine spezielle Normalverteilung transformieren kann – und zwar in eine mit solchen Parametern, die den Termen ihrer Dichte- und Verteilungsfunktion eine möglichst einfache Gestalt geben. Sigmaregeln Wahrscheinlichkeiten Normalverteilung Das Team von TheSimpleMaths erklären in ihren Nachhilfe Videos, mit tollen grafischen und didaktischen Ideen das jeweilige mathematische Thema. Standardnormalverteilung / z-Transformation Unter den unendlich vielen Normalverteilungen gibt es eine Normalverteilung, die sich dadurch ausgezeichnet ist, dass sie einen Erwartungswert von μ = 0 und eine Streuung von σ= 1 aufweist. Erläuterung der Normalverteilung und der Standardnormalverteilung sowie wie man die Wahrscheinlichkeit von Intervallen bestimmt und wie die z-Werte für die kumulative Verteilungsfunktion bestimmt werden. Sigma-Umgebungen Zusammenhang zwischen Wendepunkt der Wahrscheinlichkeitsfunktion einer Normalverteilung und dem Erwartungswert Der Erwartungswert ist der Wert mit der größten Wahrscheinlichkeit. Links und rechts vom Erwartungswert gruppieren sich die restlichen normalverteilten Wahrscheinlichkeiten. Die Wendepunkte der Wahrscheinlichkeitsfunktion der 9 Konfidenzintervalle 9.0 Einführung Wie im letzten Kapital bereits erwähnt, gibt es in der Inferenzstatistik zwei Verfahren, mit deren Hilfe wir aus einer gezogenen Stichprobe die entsprechenden Populationsparameter schätzen können. Diese sind: Die Punktschätzung Die Intervallschätzung. Die Punktschätzung schätzt anhand eines erwartungstreuen Standardnormalverteilung einfach erklärt Standardverteilung Formel Standardnormalverteilung berechnen mit Beispielen mit kostenlosem Video 10. Die Gausssche Normalverteilung # Vorlesungsaufzeichnung Normalverteilung 10.1. Approximation der Binomialverteilung # Betrachten wir eine Folge von Bernoulli-verteilten Zufallsvariablen X i mit gleichem Parameter p und S n:= ∑ i = 1 n X i die Summe über die ersten n davon, so wissen wir bereits, dass S n ∼ B i n (n, p), also dass diese Summe Binomialverteilt Mathematik Tutorial. Interaktive grafische Darstellung der Gauß-Verteilung (Normalverteilung) und Fit der Gausskurve an Messwerte.4.1 Eigenschaften der Normalverteilung
Standardnormalverteilungstabelle