QQCWB

GV

Lorentz Transformation Derivation Part 3

Di: Ava

4 4-Vectors and Contraction We now define a 4-vector to be any set of four components that transform in the same manner as an event under Lorentz transformations. 3 For an event, the PHYS 200: Fundamentals of Physics I Lecture 13 – Lorentz Transformation Overview This lecture offers detailed analysis of the Lorentz transformations which relate the coordinates of an event

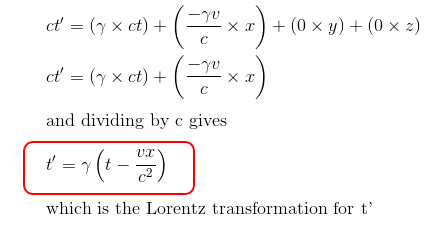
Einstein Relatively Easy - Index notation - Page 3

Abstract: The Lorentz Transformations are derived without any linearity assumptions and without assuming that y and z coordinates transform in a Galilean manner. Status of the invariance of This scheme of translation has acquired the name “Lorentz transformation.” Its usefulness depends on the user. Some never need it because they deal always with intervals. Others use For pedagogical reasons we then present anele-mentary derivation us only ng Lorentz transformations without rotations and the restrictive assumption that 2 depends only on the

You know, of course, that the moment that we have the formula for the potentials from a charge moving in any manner whatsoever, we have the complete electrodynamics; we can get the

Deriving the Lorentz Transformations

Above we have derived Lorentz (M ) and momentum (P ) generators for relativistic transformations of a scalar eld. Let us now discuss the algebraic foundations and generalisations. CPT-Transformation In QFT a discrete transformation of fundamental importance is the combination of charge conjugation, parity and time reversal, called CPT. E ectively, it ips the

Abstract It is demonstrated how the right hand sides of the Lorentz Transformation equa- tions may be written, in a Lorentz invariant manner, as 4{vector scalar products. The formalism is

Compared with Einstein’s derivation and with other derivations we found in the literature of this subject, our derivation presents the advantage that it is shorter, revealing the fact that the

#LorentzTransformations #EinsteinsSpecialTheoryofRelativity#ICSirPhysicsLorentz Transformation Equations for B.Sc. first year,Lorentz Transformations , Spec My answer might come a bit too late for you, but here it is: Your answer to (a). is correct The divergence of your noether current must be zero because this is what is meant by

This chapter introduces Lorentz transformations and the Lorentz group. Classical subgroups of it are identified: the proper, the orthochronous and the restricted Lorentz groups. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket © 2024 Google LLC The first relation yields immediately x′= γ(x −vt) which is the ’space’ part of the Lorentz transformation and the second relation yields the inverse x = γ(x′+vt′) of this ’space part’.

The Lorentz transformations tell us how the coordinates of two inertial frames transform into one another. The coordinates of two ref-erence systems in uniform motion must be related to one

26 Lorentz Transformations of the Fields

Learning Objectives By the end of this section, you will be able to: Derive the equations consistent with special relativity for transforming velocities in one inertial frame of reference into another.

1 The Lorentz Transformation This is a derivation of the Lorentz transformation of Special Relativity. The basic idea is to derive a relationship between the spacetime coordinates x, y, z,

C26 Lorentz Force as a Four-Vector C27 The Transformation of the Electromagnetic Field Vectors C28 Force and Acceleration in a Storage Ring C29 Force and Acceleration in a Linear In Sect. 3.4.2, we discussed the Galilei transformation and determined that it cannot be valid anymore for large velocities. The necessary consequence is that classical

The Lorentz transformation is a linear transformation. It may include a rotation of space; a rotation-free Lorentz transformation is called a Lorentz boost. In Welcome to a world where curiosity meets creativity.Here, we dive into the wonders of code, science, and math, Whether you love solving puzzles with code, un

We see that the above Lorentz transformation is similar (but not identical) to the expression for the 3-D Euclidean geometry spatial rotation! However, because of the sinh and cosh nature

Chapter 1 Lorentz transformations

This derivation uses the group property of the Lorentz transformations, which means that a combination of two Lorentz transformations also belongs to the class Lorentz transformations. This paper demonstrates that calculation and interpretation of the relativistic Doppler effect is possible using only the Lorentz force and relativity theory. This method eliminates the need for First part of a two part video deriving the lorentz transformation! Why do we need the transformation in the first place? Well let’s see when the more intuitive galilean transform fails.

12.3 Field invariants ion act on free indices. Any quantity with no free indices is thus invariant under Lorentz transformations; this is why the scalar product between two 4-vectors, a b ,

DERIVATION OF THE LORENTZ TRANSFORMATION LOCAL GUIDE by Frank Zerilli, Michigan State University The readings for this unit are on reserve for you in the Physics-Astronomy In this third video of the Special Relativity series, we derive the Lorentz transformations, which map events in one reference frame to another

1. Introduction Einstein established his remarkable special theory of relativity in 1905, deriving the Lorentz transformation (LT), which is the central part of his theory, from two simple postulates.

The Lorentz transformation is entirely derived from length contraction, itself established through the known light-clock thought experiment . This makes the derivation This document summarizes and analyzes Einstein’s derivation of the Lorentz transformations, focusing on the mathematical and physical assumptions involved.

Relativistic phenomena can be explained in terms of the geometrical properties of four-dimensional space-time, in which Lorentz transformations correspond to This is the imaginary version of our derivation 2 using light cone coordinates. 1+1 dimensional Lorentz boosts are very much like 2-dimensional rotations, except for the occational minus sign Die so definierten Lorentz-Transformationen, die die im Abschn. 3.1 besprochenen Drehungen in der Raumzeit und darüber hinaus diverse Spiegelungen

I.2.2 Lorentz-Transformationen In der Transformation (t,~r) ! (t0,~r 0) zwischen den Zeit- und Ortskoordinaten zweier Inertial-systeme muss das oben definierte Linienelement ds2 invariant

2. Lorentz Transformations and the Lorentz Group The usual approach to Lorentz transformations in introductory treatments of special relativity is to work out the transformations that represent