QQCWB

GV

Generalized Linear Model For Binomial Data

Di: Ava

To overcome this problem, the NB-Lindley (NB-L) distribution has recently been introduced for analyzing count data that are characterized by excess zeros. The objective of this paper is to document the application of a NB generalized linear model with Lindley mixed effects (NB-L GLM) for analyzing traffic crash data. GLM: Binomial response data Load Star98 data In this example, we use the Star98 dataset which was taken with permission from Jeff Gill (2000) Generalized linear models: A unified approach. Codebook information can be obtained by typing:

Binomial – Towards Data Science

Traditionally, the random component is a univariate “exponential family” — the normal (Gaussian), binomial, Poisson, gamma, or inverse-Gaussian family of distributions — but generalized linear models have been extended beyond the univariate exponential families.

Generalized linear Regression Models

Introduction Generalized Linear Models (GLMs) are a cornerstone in statistical analysis and data science, extending traditional linear models to The first widely used software package for fitting these models was called GLIM. Because of this program, „GLIM“ became a well-accepted abbreviation for generalized linear models, as opposed to „GLM“ which often is used for general linear models. Today, GLIMs are fit by many packages, including SAS’s Genmod procedure and R’s glm () function.

As expansions of LMMs, generalized linear mixed models (GLMMs) can be used to analyze the data arising from several non-normal statistical distributions, including the discrete binomial, Poisson, and negative binomial, as well as the continuous gamma and beta.

The same problem occurs with Wald tests for binomial, Poisson and negative binomial generalized linear models with logit or log-link functions when one of the groups being compared has all zero counts and the corresponding coefficient becomes infinite. The exponential family of distributions is very broad and contains many important distributions. For example, the binary, binomial, Poisson, negative binomial, normal, beta, gamma, and inverse Gaussian distribution are members of this family. A special case of the generalized linear model arises when the Yi are normally distributed and the link function is the identity function. The

I have proportional data that takes any value from 0 and 1. However, there are certainly an over-abundance of zeroes, and the rest of the values (there are few) tend to be close to zero. I’m wondering with this knowledge what is the appropriate GLM to use? Generalized linear models (Ch. 4) We saw that the Bernoulli \ ( (\pi)\) family is an exponential family with natural parameter \ [ \log \left (\frac {\pi} {1-\pi Introduction Generalized linear models (GLMs) stand as a cornerstone in the field of statistical analysis, extending the concepts of

Description glm fits generalized linear models. It can fit models by using either IRLS (maximum quasilikelihood) or Newton–Raphson (maximum likelihood) optimization, which is the default.

Introduction Generalized Linear Models (GLMs) represent a cornerstone in the landscape of statistical analysis, extending the capabilities of traditional linear models to accommodate a variety of data distributions beyond the conventional normal distribution.

Generalized Linear Model Distribution and Link Function Selection

1.2 Linear Regression Model Before we explore the generalized regression models, it is a good idea to start with linear regression model to understand why and how we extend the linear regression model to generalized linear regression models.

  • Generalized linear models
  • Introduction to Generalized Linear Models
  • Introducing the GLIMMIX Procedure for Generalized Linear Mixed Models
  • Generalized Linear Models
  • Generalized Linear Models: A Comprehensive Introduction

Estimating Generalized Linear Models for Count Data with rstanarm 2024-01-16 Introduction Likelihood Priors Posterior Poisson and Negative Binomial Regression Example References

GLMs (generalised linear models) allow the analysis of count or bounded data. This post will show you how to use them to analyse binary data in R!

Generalized Linear Mixed-Effects Models (GLMMs) are powerful statistical models used to analyze data with non-normal distributions, hierarchical structures, and correlated observations. These models extend the capabilities of Generalized Linear Models (GLMs) by incorporating random effects to account for variability at multiple levels. Checking assumptions on a model that you know is inappropriate, seems a futile exercise, unless better alternatives are available, and that is the case: with Generalized Linear Models (GLMs) we extend our regression modeling framework once again, this time focusing on the outcome variables and their shape of randomness.

Lecture 12: Generalized Linear Models for Binary Data Dipankar Bandyopadhyay, Ph.D. BMTRY 711: Analysis of Categorical Data Spring 2011 Division of Biostatistics and Epidemiology Medical University of South Carolina

Generalized linear models (GLM’s) are a class of nonlinear regression models that can be used in certain cases where linear models do not t well. Logistic regression is a speci c type of GLM. We will develop logistic regression from rst principles before discussing GLM’s in general. Generalized linear models use linear methods to describe a potentially nonlinear relationship between predictor terms and a response variable.

Introduction Generalized Linear Models (GLMs) represent an extension of traditional linear regression models designed to accommodate a wide array of data types and distribution patterns. This flexibility makes GLMs indispensable in the arsenal of data scientists and statisticians. At their core, GLMs consist of three principal GLMs (Generalized linear models) are a type of statistical model that is extensively used in the analysis of non-normal data, such as count data GLM: Binomial response data Load Star98 data In this example, we use the Star98 dataset which was taken with permission from Jeff Gill (2000) Generalized linear models: A unified approach. Codebook information can be obtained by typing:

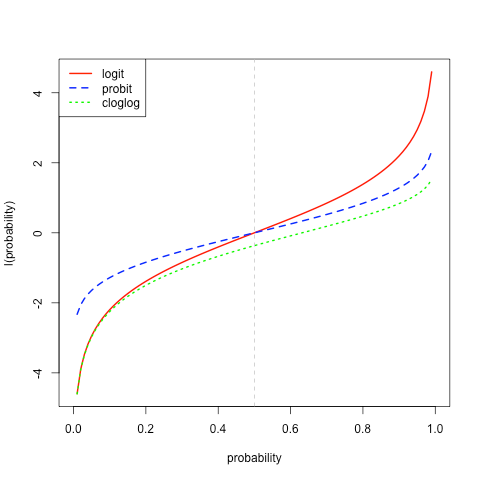
GLMs: scope Generalized linear models include many familiar model types, for example: Linear models. Identity link, normal distribution. Models for analysis of contingency tables. Log link, Poisson distribution. Logistic regression. ‘logit’ or ‘probit’ link, binomial distribution. The logistic regression model is an example of a broad class of models known as generalized linear models (GLM). For example, GLMs also include linear regression, ANOVA, poisson regression, etc. However, an LM is not suitable for modeling a binary response, an ordinal response with few levels or a response that represents a count. For these we use generalized linear models (GLMs). To describe GLMs we return to the representation of the response as an n-dimensional, vector-valued, random variable, Y.

I. Motivation In this lecture we extend the ideas of linear regression to the more general idea of a generalized linear model (GLM). The essence of linear models is that the response variable is continuous and normally distributed: here we relax these assumptions and consider cases where the response variable is non-normal and in particular has a discrete distribution. Although For generalized linear models, we are always modeling a transformation of the mean by a linear function of X, but this will change for generalized additive models Now it helps to go through several examples Binomial GLM We want to measure the impact of watching tv-shows on the probability of passing the statistics exam.

Chapter 7 introduces one of the most useful statistical frameworks for the modern life scientist: the generalized linear model (GLM). GLMs extend the linear model to an array of non-normally distributed data such as Poisson, negative binomial, binomial, and Gamma distributed data. 13 The interpretation is the same as for a generalised linear model, except that the estimates of the fixed effects are conditional on the random effects. Since this is a generalized linear mixed model, the coefficient estimates are not A semiparametric negative binomial generalized linear model for modeling over-dispersed count data with a heavy tail: Characteristics and applications to crash data Mohammadali Shirazi a , Dominique Lord a , Soma Sekhar Dhavala b , Srinivas Reddy Geedipally c Show more Add to Mendeley

Generalized Linear Models Generalized linear models currently supports estimation using the one-parameter exponential families. See Module Reference for commands and arguments. Examples