Fitting Data To Binomial Or Bernoulli Distributions
Di: Ava
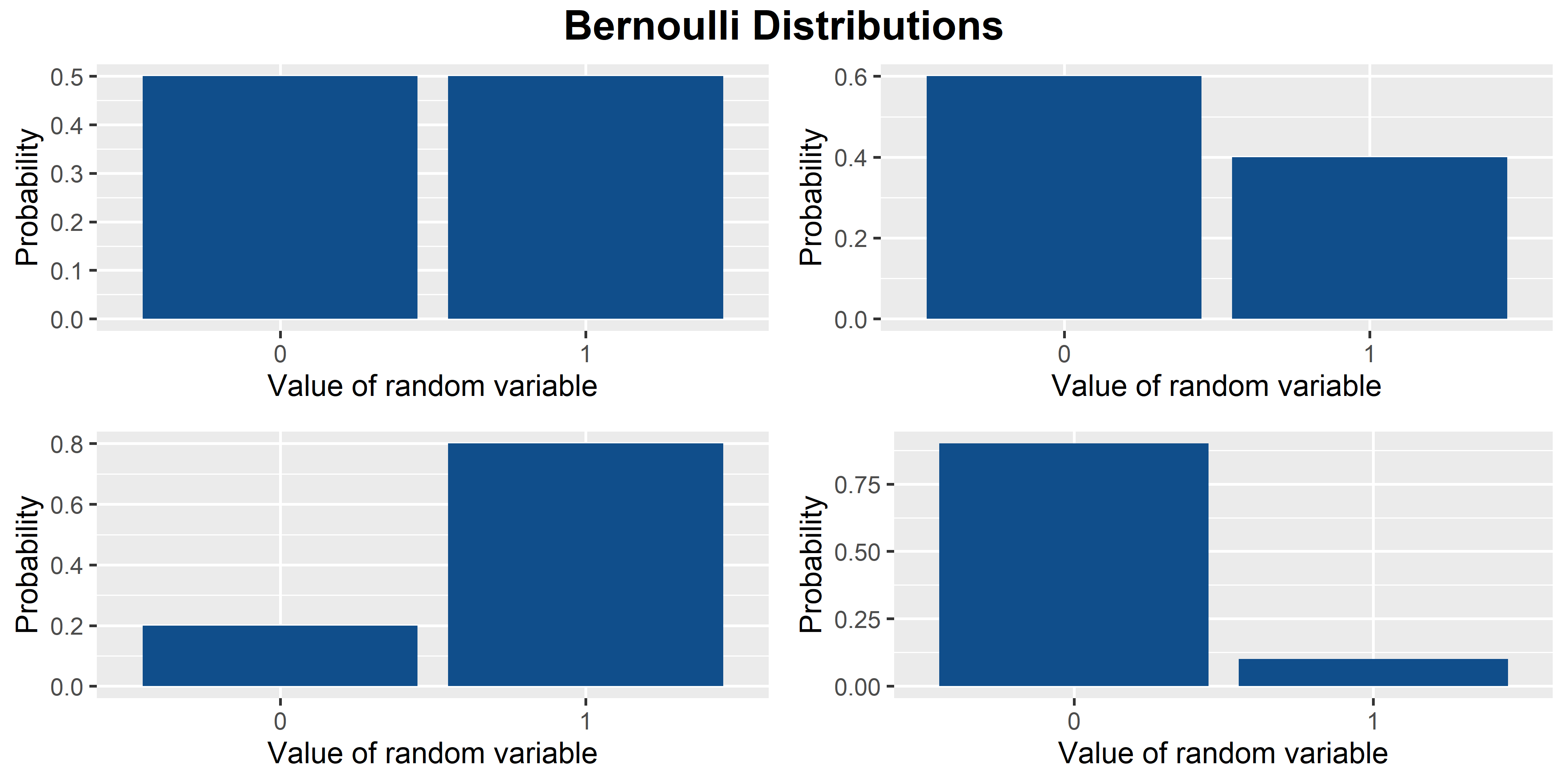
The Bernoulli distribution is the binomial distribution with one trial and can be used to simulate Yes/No or Success/Failure conditions. This distribution is the fundamental building block of other more complex distributions. Create a probability distribution object BinomialDistribution by fitting a probability distribution to sample data or by specifying parameter values. Then, use object functions to evaluate the distribution, generate random numbers, and so on. Work with the binomial distribution interactively by using the Distribution Fitter app.
The Binomial Distribution
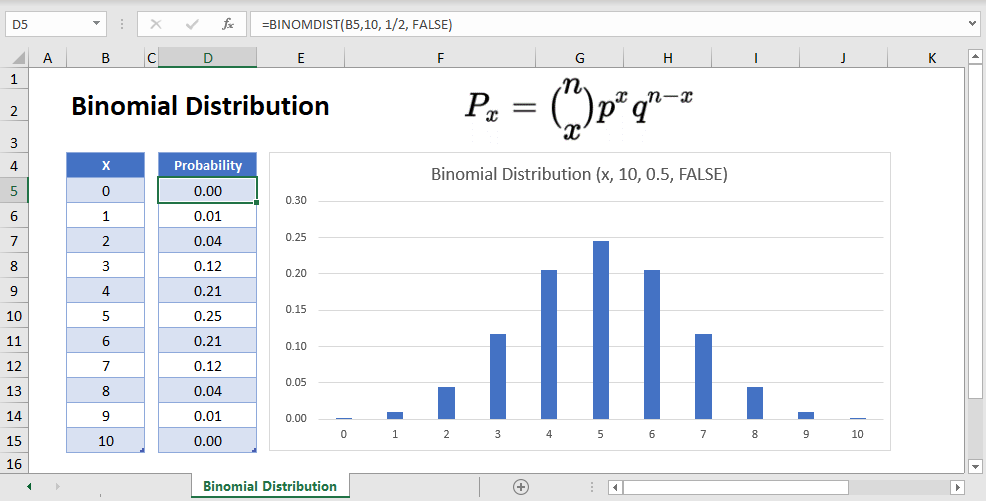
A more valuable probability density function with many applications is the binomial distribution. This distribution will compute probabilities for any binomial process. A binomial process, often called a Bernoulli process after the first person to fully develop its properties, is any case where there are only two possible outcomes in any one trial, called successes and
If the data has a binary response, we might want to use the Bernoulli or Binomial distributions. If we are working with count data, a Poisson model might be more useful. Univariate distributions are the distributions whose variate forms are Univariate (i.e each sample is a scalar). Abstract types for univariate distributions:
A Bernoulli distribution is a probability distribution for scenarios with two possible outcomes, such as success or failure, often used in machine learning. A. Typical types of distribution in data science include normal (Gaussian), uniform, exponential, Poisson, and binomial distributions, each characterizing the probability patterns of different types of data. Binomial distribution is a statistical distribution used to model the number of successful outcomes in a fixed number of independent trials with a constant probability of success. In R programming, the binomial distribution is an important probability distribution function that can be easily calculated using built-in functions such as dbinom, pbinom, and qbinom. Whether you’re a
Bernoulli Distribution — A simple distribution dealing with binary (yes/no, success/failure) outcomes. Binomial Distribution — An extension of the Bernoulli distribution that models multiple The binomial distribution is useful for describing distributions of binomial events, such as the number of males and females in a random sample of companies, or the number of defective components in samples of 20 units taken from a production process. The standard model to fit binomial (0/1 or k/n) data is the logistic regression, which combines the binomial distribution with a logit link function. To get to know this model, let’s have a look at the titanic data set in EcoData:
Create a probability distribution object BinomialDistribution by fitting a probability distribution to sample data or by specifying parameter values. Then, use object functions to evaluate the distribution, generate random numbers, and so on. Work with the binomial distribution interactively by using the Distribution Fitter app. GeeksforGeeks | A computer science portal for geeks The outcomes of a binomial experiment fit a binomial probability distribution. The random variable \ (X =\) the number of successes obtained in the \ (n\) independent trials.
- Probability Data Distributions in Data Science
- GNU Octave: Distributions
- The Binomial Distribution
- Difference Between Binomial and Poisson Distribution
Hence, we can relate the probability of infestation modelled through the logit-link to our data using a binomial distribution with one trial, which translates into the Bernoulli distribution (a special case of the binomial distribution with only one trial): The number of observations in each row is the number of Bernoulli trials, and so data entered like this come from a binomial distribution. Regardless of whether your logistic regression is based on Bernoulli or Binomial outcome variables, in both cases, we’re interested in how the predictors relate to p, the probability of success. Furthermore, the binomial distribution, the successor to the Bernoulli distribution, can be used to answer questions about probabilities that were previously impractical.
The Bernoulli distribution, which takes value 1 with probability p and value 0 with probability q = 1 − p. The Rademacher distribution, which takes value 1 with probability 1/2 and value −1 with probability 1/2. The binomial distribution, which describes the number of successes in a series of independent Yes/No experiments all with the same probability of success. The beta-binomial The present block is devoted to the study of some special discrete distributions and in this list, Bernoulli and Binomial distributions are also included which are being discussed in the present unit of the course.
In logistic regression where classification outputs are binary, Bernoulli and Binomial distributions are utilized alongside cross-entropy cross This guide aims to provide a clear understanding of binomial distributions, their properties, and how they are applied in data science and Binomial and Poisson distributions are two important types of discrete probability distributions used in statistics and data analysis. binomial distribution models the number of successes in a fixed number of independent trials, each with the same probability of success.
Introduction Fitting a distribution to data in Excel is a crucial task in data analysis and statistical modeling. By understanding the distribution of your data, you Bernoulli Distribution Binomial Distribution Implement Bernoulli Distribution With the Help of NumPy in Python As a really important topic in Statistics, the Bernoulli distribution is an essential aspect of Data Science, Machine Learning, and other related fields because it helps deal with data. This tutorial will demonstrate the Bernoulli distribution and how it can be
Understanding how data behaves is one of the first steps in data science. Before we dive into building models or running analysis, we need to understand how the values in our dataset are spread out and that’s where probability distributions come in. Let us start with a simple example: If you roll a fair die, the chance of getting a 6 is 1 out of 6, or 16.67%. This is a basic
Excel has got many features connected with statistics. For examples Excel could help you to calculate binomial distribution (aka bernoulli distribution). Let’s learn how to do it in this easy steps. On the other hand, the multivariate Bernoulli distribution has an interesting property in that independence and uncorrelatedness of the component ran-dom variables are equivalent. Both the marginal and conditional distributions of a subset of variables in the multivariate Bernoulli distribution still follow the multivariate Bernoulli distribution. GNU Octave: DistributionsFor each element of x, compute the quantile (the inverse of the CDF) at x of the binomial distribution with parameters n and p, where n is the number of trials and p is the probability of success.
The Binomial distribution, on the other hand, extends this to multiple trials, each following a Bernoulli distribution. Parameter: The Bernoulli distribution has a single parameter, p, representing the probability of success on each trial. In probability theory and statistics, the negative binomial distribution, also called a Pascal distribution, [2] is a discrete probability distribution that models the number of failures in a sequence of independent and identically distributed Bernoulli trials before a specified/constant/fixed number of successes occur. [3] For example, we can define rolling a 6 Binomial Distribution – 15 – Expected Frequencies and Fitting of binomial distribution PUAAR Academy 50.2K subscribers 1.8K
This lets you enter historical data; then @RISK attempts to fit every relevant distribution to the data. You can instantly compare different distributions to see which one seems best suited to the data set. If you’re not fitting to existing data, here are some things to think about: Create a probability distribution object BinomialDistribution by fitting a probability distribution to sample data (fitdist) or by specifying parameter values (makedist). Then, use object functions to evaluate the distribution, generate random numbers, and so on. Work with the binomial distribution interactively by using the Distribution Fitter app. You can export an object from the I want to perform logistic regression with the following binomial response and with $X_1$ and $X_2$ as my predictors. I can present the same
I have a series of data to which I want to fit my model. The model predicts the probability of success at a given value of x. I have a single data point at a number of points in this space. As I have a single point which is either pass or fail with a certain probability I believe I should fit using a Bernoulli maximum likelihood fit, is this correct? So i have a likelihood function which looks
Binomial distribution questions for Class 12 with solutions are provided here for practice. Before understanding the concept of the binomial distribution, let us understand some facts about binomial experiments. There are some sorts of experiments which have only two possible outcomes, either a “ success ” or a “ failure ” – these types of random experiments are called
Fitting data # To fit data to a distribution, maximizing the likelihood function is common. Alternatively, some distributions have well-known minimum variance unbiased estimators. These will be chosen by default, but the likelihood function will always be available for minimizing.
- Flash Externo Para Principiantes: Conociendo Cómo Funciona
- Fitness-Übungen: Training Entschlackung Der Beine
- Fitnessübungen Berufskraftfahrer
- Fischereiverein Wattenscheid 1964 E. V. In Bochum
- Fiscalidad En Luxemburgo: Régimen Fiscal De Las Personas Físicas
- Five Examples Of Predictive Maintenance In Action
- Fitbit Ionic Review: Bridging Fitness Tracker And Smartwatch Divide
- Five Decades Of Fighting: Roberto Durán
- Flammend‘ Herz Flensburg, Tattoo-Piercing, Flensburg
- Flags Of Countries Beginning With : T
- Five German Shepherd Health Issues You Need To Know About
- Flag Of El Salvador » God, Union And Liberty.