QQCWB

GV

Fdu 回归分析 3. Ridge回归 , Lasso回归（概念+实例）-CSDN博客

Di: Ava

文章浏览阅读1.4k次，点赞23次，收藏25次。简介：Logistic回归模型是统计学中用于二分类问题的重要工具，通过线性回归与对数几率函数的结合，将预测结果转换为概率值。本文介绍了该模型的基础、形式、参数估计、评估、应用、扩展、优缺点、局限性以及模型的选择与优化方法。特别强调了Logistic

岭回归（Ridge）分析概述 岭回归是一种正则化线性回归模型，用于解决线性回归模型中可能出现的过拟合问题。 它通过在损失函数中添加一个惩罚项来实现正则化，该惩罚项与模型系数的 L2 范数成正比。 FDU 回归分析 1. 简单线性回归 (3) 置信区间估计 & 假设检验 Snivellus Snape 科研行业 从业人员

Lasso回归（概念+实例）-CSDN博客

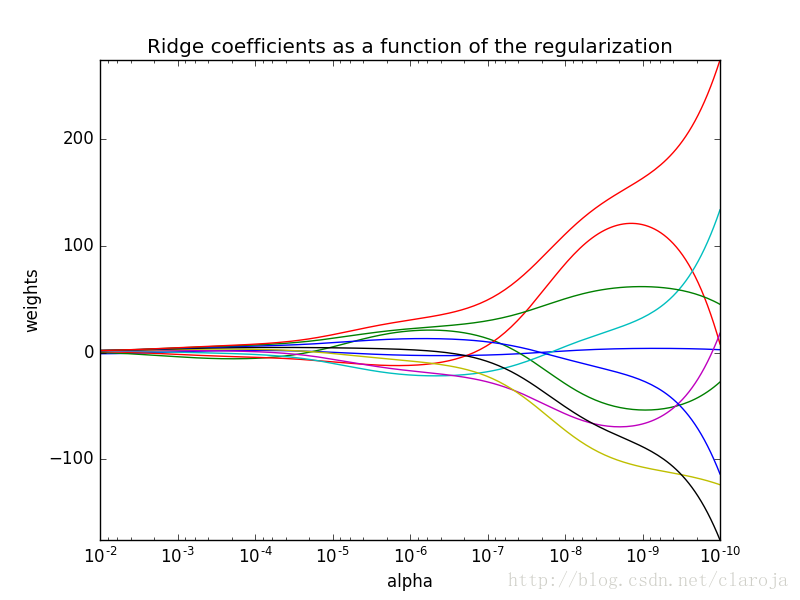
Python回归 岭回归（Ridge Regression）-CSDN博客

2.2.3.4 Mini-batch 2.3 机器学习的简单示例：线性回归 线性回归（Linear Regression）是机器学习和统计学中最基础和广泛应用的模型，是一种对自变量和因变量之间关系进行建模的回归分析。 自变量数量为 1时称为简单回归，自变量数量大于 1时称为多元回归。 2.3.1 前言：网上关于各种回归分析，无论是lasso还是ridge都挺多，但许多也都泛泛而谈，然后给一段python或者R代码，最后加上各种reference以及广告。当然，

本文根据王勤文老师课堂笔记整理而成，欢迎批评指正！ 第一部分内容参见：FDU 回归分析 2. 多元线性回归 (1) 模型参数的无偏估计量第二部分 简介给定 [toc] 1.前言 1.1 岭回归的介绍 岭回归（Ridge Regression）是一种常用的线性回归方法，用于处理具有共线性（collinearity）问题的数据集。在普通最小二乘线性回归中，如果自变量之间存在高度相关性，会导致估计的回归系数不稳定，甚至无法准确估计。岭回归通过引入一个正则化项来解决这个问题。 岭

文章浏览阅读5.7k次，点赞10次，收藏41次。该博客围绕线性回归实验展开，在Anaconda的jupyter notebook上用Python实现。先介绍一元和三元线性回归模型的实验要求与数据预处理，再分别用最小二乘法、梯度下降法、矩阵求解法进行拟合，并分析结果。最后总结线性回归概念及三种算法特点与适用场景。 岭回归（Ridge Regression），也被称为Tikhonov正则化，是一种线性回归的变体。 它通过在普通最小二乘法（OLS）回归中加入L2正则化项来解决多重共线性问题，从而提高模型的泛化能力和鲁棒性。 目录 前言 一、基本概念 1.1Lasso回归的起源和动机 1.2数学表达 1.3参数λ的影响 1.4Lasso的计算方法 1.5Lasso与Ridge回归的比较 1.6Lasso的优点和缺点 1.7应用领域 二、具体实例

  • 极智分析保姆级教学：lasso回归
  • 用Python实现9大回归算法详解——03. 岭回归算法
  • 什么是LASSO回归，怎么看懂LASSO回归的结果-CSDN博客

Ridge 回归是一种用于处理多重共线性（即自变量之间高度相关）的线性回归技术。它通过在模型中引入一个额外的惩罚项来避免过拟合，从而提高模型的泛化能力。 那么，具体什么是 Ridge 回归？ 一、Ridge回归的起源与思想 Ridge回归，又称岭回归，是一种经典的线性回归方法，旨在解决多重共线性问题。多重共线性是指自变量之间存在高度相关性，导致回归系数的估计不稳定。Ridge回归通过引入L2正则化项，对回归系数进行约束，从而提高模型的稳定性和泛化能力。 文章浏览阅读1.3k次，点赞27次，收藏14次。多元线性回归；最小二乘法求解多元线性回归；矩阵求解最小二乘法；梯度下降法；多重共线性；Lasso回归；Ridge回归；多项式回归_多元线性回归代理模型

文章目录 【机器学习|回归算法】线性回归、逻辑回归、Lasso 回归、Ridge 回归详解，附代码。 ? 1. 线性回归（Linear Regression） ? 起源 ⚙️ 原理 ? 公式 优点 缺点 ? 应用 ? Python代码 ? 2. 逻辑回归（Logistic Regression） ? 起源 ⚙️ 原理 ? 公式 优点 缺点 ? 应用 ? Python代码 ? Lasso 可以用于变量数量较多的大数据集。 传统的 线性回归模型 无法处理这类大数据。 虽然 线性回归估计器 (linear regression estimator)在偏-方差权衡关系方面是无偏估计器，但 正则化 或 惩罚回归，如 Lasso, Ridge 承认一些减少方差的偏倚。 在本篇文章当中主要给大家深入介绍线性回归算法以及扩展的Lasso和Ridge回归，以及他们能够有效的原因！！

FDU 最优化方法 要素察觉：江如俊老师 孩子们，刘导有我剩下的笔记 Snivellus Snape

在R中，可以通过glmnet包中相关函数建立Ridge回归和Lasso回归模型。 1 使用R进行Ridge回归 例1 糖尿病病情数据集（diabetes.csv）包含442个样本，每

【回归预测】多元岭回归 (Ridge Regression) -MATLAB - 知乎

Lasso 回归也叫套索回归，是通过生成一个惩罚函数是回归模型中的变量系数进行压缩，达到防止过度拟合，解决严重共线性的问题，Lasso 回归最先由英国人Robert Tibshirani提出，目前在预测模型中应用非常广泛。新格

本文深入探讨线性回归的核心概念，包括简单线性回归、多元线性回归、逐步回归、多重共线性分析、正则化及逻辑回归。通过代码示例、FAQ及概念对比，帮助读者全面掌握线性回归的应用与原理。 一、基于原生Python实现岭回归 (Ridge Regression) 岭回归（Ridge Regression）是一种常见的 线性回归 的扩展形式，它通过引入 L2正则化 项

本文根据王勤文老师课堂笔记整理而成，欢迎批评指正！第一部分 简介回归分析的任务是根据观测 (x_1,y_1),(x_2,y_2),,(x_n,y_n) 来推断随机变量 X, Y 之间的关系，并根据推断的结果做预测. Y 称为响应变量 (resp 回归分析期末试题及答案-2.使用最小二乘法求解简单线性回归模型的参数估计值。最小二乘法是一种常用的回归分析方法，用于估计回归模型中的参数值。以简单线性回归模型Y = β0 + β1X为例，最小二乘法通过最小化观测值Y与模型预测值之间的平方差来估计β0和β1。3.请计算多元线性回归模型的回归 文章浏览阅读4.8w次，点赞71次，收藏344次。本文介绍了弹性网络回归，一种结合岭回归和Lasso回归优点的模型，通过λ和ρ参数控制正则化，利用坐标下降法求解。通过实例演示和代码实现，展示了其在特征选择与稳定性的平衡作用，并以音乐转谱应用举例。

岭回归分析（Ridge Regression）用于解决线性回归分析中自变量共线性的研究算法。 岭回归通过引入k个单位阵，使得回归系数可估计；单位阵引入会导致信息丢失，但同时可换来回归模型的合理估计。 所以，LASSO回归高效解决了筛选变量的难题：区别于传统的逐步回归stepwise前进、后退变量筛选方法，LASSO回归可以利用较少样本量，高效筛选较多变量。 比如在基因组学、影像学、以及其他小样本分析中，LASSO回归都可以派上大用场。 2.LASSO在SCI文章中的 2. 所有参数的平方和，即L2范数，对应的回归方法叫做Ridge回归，岭回归 岭回归对应的代价函数如下 lasso回归对应的代价函数如下 红框标记的就是正则项，需要注意的是，正则项中的回归系数为每个自变量对应的回归系数，不包含回归常数项。

广播电视节目制作经营许可证:（京）字第06591号 互联网宗教信息服务许可证：京（2022）0000078

注意事项: 本课程有一次期中考试（11月10日, 星期三）。期中考试没有补考，缺席按零分记。出现身体疾病（急症）的情况 (必须出示本校医院诊断书），可以例外，其期中所占比例转到期末考试。 作业是学习过程的一个重要部分，希望大家认真对待。支持同学间的讨论，但严厉杜绝作业抄袭 文章浏览阅读1.8k次，点赞14次，收藏22次。LASSO 回归和 Ridge 回归通过对损失函数施加正则化项的方式，使得回归建模过程中大量不重要的特征系数被压缩为 0 或者接近 0 ，从而找出对目标变量有较强影响的关键特征。_lasso回归模型 岭回归 （Ridge Regression），又称为 Tikhonov 正则化，是一种线性回归模型，它通过引入 L2 L 2 正则化来防止模型过拟合。 与 Lasso 回归不同，岭回归不会将系数缩减为零，而是通过缩小系数的大小来控制模型复杂度，从而增强模型的泛化能力。

岭回归 (Ridge Regression) 是一种线性回归模型的改进方法，专门用于解决多重共线性问题以及提高模型的泛化能力。在传统的线性回归中，当特征之间存在较强的相关性时，模型的系数会变得不稳定，甚至可能导致过拟合。岭回归通过加入正则化项 (regularization term) 来约束回归系数的大小，从而有效

简单线性回归 (2) 模型参数的无偏估计量 (2)整理了王勤文老师的课堂笔记，欢迎指正！ 第一部分 总结：最小均方估计量 最小均方估计量是均方误差 SSE 的最小值点，其梯度的零点满足特定条件。 本文根据王勤文老师课堂笔记整理而成，欢迎批评指正！第一部分 总结：最小均方估计量 \\hat \\alpha, \\hat \\beta \\begin{equation

岭回归（Ridge Regression）是一种用于处理多重共线性的有偏估计回归方法，它是最小二乘估计法的一种改良。 岭回归的主要目的是解决线性回归中的多重共线性问题，即当自变量之间高度相关时，普通最小二乘法可能导 5.1.1 回归分析的含义 “回 归”这 一术语最早是由英国统计学家高尔顿(FrancisGalton)19在世纪末期研究人类遗传问题时提出的。 他发现,总 体上子辈身高和父辈身高是正相关的,但是当父辈身高异常高或异常矮时,子 辈高于或矮于父辈的概率很小。他将子辈身高向父辈的平均身高回归的趋势移动 文章浏览阅读8.2k次，点赞18次，收藏52次。本文详细阐述了一元线性回归模型的建立、参数估计方法（最小二乘法）、性质（无偏性与有效性）及显著性检验（t检验和F检验）。随后扩展至多元线性回归，介绍了基本假定、参数估计过程以及回归方程的显著性检验。此外，还涵盖了中心化和