Ereignisse Und Diskrete Wahrscheinlichkeitsräume

Di: Ava

Diskrete Stochastik: Ereignisse und ihre Wahrscheinlichkeiten; diskrete Wahrscheinlichkeitsräume; Zufallsvariablen; Erwartungswert und Varianz; Markov-Ungleichung; Tschebyscheff-Ungleichung; Ausblick auf randomisierte Algorithmen und deren erwartete Laufzeit bzw. Erfolgswahrscheinlichkeit 4 Kapitel I Diskrete Wahrscheinlichkeitsräume Indem wir Wahrscheinlichkeiten nur im Modell defmiert haben, sind wir der Frage, was Wahrscheinlichkeiten eines realen Ereignisses sind, aus dem Weg gegangen. In diesem Buch werden wir ausschließlich diskrete Ergebnisräume betrachten, deshalb der Titel „Diskrete Wahrscheinlichkeitsrechnung“. Damit werden wir einen Überblick über den Inhalt der Wahrscheinlichkeitsrechnung und eine Basis für das weitere Studium der allgemeinen Theorie erhalten. Ein Experiment veranlasst bestimmte Ereignisse.

M1K Diskrete Strukturen für das Lehramt Informatik

n klar und wird uns noch viel beschäftigen. Die oben genannten „Axi ealer Ereignisse sind, aus dem Weg gegangen. Man versteht wohl allgemein die Wahrscheinlichkeit eines realen Ereignisses als Maß für die Sicherheit oder Häufigkeit, mit der es bei wiederholte

Definition: diskreter Wahrscheinlichkeitsraum ...

Ein Versuch in diese Richtung würde die Wahrscheinlichkeit eines Ereignisses E als den Erwartungswert der relativen Häufigkeit des Eintretens von E definieren, also als den Quotienten aus der Zahl der Fälle in denen E eingetreten ist und der Gesamtlänge der “Versuchsreihe”, den man bei einer sehr langen Reihe gleichartiger Situationen erwarten würde. Diese Definition –

Seien ( 1; P1) und ( 2; P2) diskrete Wahrscheinlichkeitsräume. Der Produktraum ist das #kartesische Produkt Ich beginne daher mit Produktexperimenten als Modell unabhängiger Ereignisse und ersten Anwendungen auf Ausfallwahrscheinlichkeiten. Nach Einführung der Urnenmodelle kommen wir zu Stichproben und damit zu hypergeometrischen, Binomial- und Poisson–Verteilungen.

In der Vorlesung werden die folgenden Themen behandelt: Diskrete Wahrscheinlichkeitsräume (Ereignisse, Zufallsvariablen und ihre Verteilungen, Grundlagen der Kombinatorik, Kenngrößen von Verteilungen, bedingte Wahrscheinlichkeiten, stochastische Unabhängigkeit, Grenzwertsätze) Allgemeine Wahrscheinlichkeitsräume (sigma-Algebra,

Elementare Wahrscheinlichkeitstheorie (LA/BA) WS 2011/12 Gliederung (aktuell/geplant) Einleitung I. Diskrete Wahrscheinlichkeitsmodelle 1. Zufällige Versuche und zufällige Ereignisse zufällige Versuche Verknüpfung von Ereignissen Zusammenhang: Zufällige Ereignisse und Teilmengen σ-Algebren (Potenzmengen) 2. Wahrscheinlichkeiten und Zufallsgrößen

Lehr- und Handbücher der Statistik

WAHRSCHEINLICHKEITS- THEORIE I WAHRSCHEINLICHKEITS- THEORIE I MEHR ANZEIGEN ePAPER LESEN ePAPER HERUNTERLADEN TAGS verteilung kapitel beliebige seien funktion wahrscheinlichkeit definition eigenschaften ereignisse dichte theorie www3.math.tu.berlin.de

Grundzüge der diskreten Wahrscheinlichkeitsrechnung
Diskrete Wahrscheinlichkeitstheorie Repetitorium
Stochastik für Einsteiger

In diesem Abschnitt wird eine Wahrscheinlichkeitsfunktion mit Hilfe der Axiome von Kolmogorow eingeführt, die zusammen mit der Ergebnismenge und dem Ereignisraum einen Wahrscheinlichkeitsraum bilden. Zufallsvariablen können diskrete oder kontinuierliche Werte annehmen. Die mathematische Beschreibung unterscheidet sich, da die 5.1 Diskrete Wahrscheinlichkeitsräume Was versteht man unter einem endlichen Wahrscheinlichkeitsraum? (ii) Geben Sie Beispiele solcher Räume an, dabei auch Modelle für Laplace-Experimente!

Stetige und diskrete Wahrscheinlichkeitsverteilungen - Minitab

Inhalt dieses Kapitels T Diskrete Wahrscheinlichkeitsräume Zufall und Wahrscheinlichkeit: Grundbegriffe Rechnen mit Ereignissen: Wahrscheinlichkeitsräume Bedingte Wahrscheinlichkeit und Unabhängigkeit Bedingte Wahrscheinlichkeiten, Formel von Bayes Stochastische Unabhängigkeit von Ereignissen

Elementare Kombinatorik und diskrete Wahrscheinlichkeitsräume Kombination von Ereignissen, unabhängige Ereignisse, bedingte Wahrscheinlichkeiten Wichtige diskrete und stetige Modelle Zentrale Begriffe der WR: Zufallsvariable, Verteilung, Momente, char. Funktion Konvergenzbegriffe Gesetze der Großen Zahlen, der Zentrale Grenzwertsatz 6 Diskrete Wahrscheinlichkeitsräume In diesem und dem folgenden Kapitel befassen wir uns mit der Frage, wie man Wahrscheinlichkeitsverteilungen formelmäßig beschreiben kann, bzw. welche minimale Menge an Information man über eine Wahrscheinlichkeitsverteilung besitzen muss, um wenigstens im Prinzip die Wahrscheinlichkeit M1.1 Diskrete Strukturen (1. Teil des Moduls M1: Mathematik für die Informatik 1) – Detailseite Funktionen: Seiteninhalt: Grunddaten Termine Zugeordnete Person Studiengänge Einrichtungen Inhalt Strukturbaum

Text Vorschau Technische Universität Berlin Wahrscheinlichkeitstheorie I Fakultät II Institut für Mathematik Sommersemester 2025 Prof. Dr. Wolfgang König, Thorsten Lucke Übungsblatt Nr. 1 Diskrete Wahrscheinlichkeitsräume Für die Woche vom 21. 25. April 2025 Aufgabe 1. Sei Ω Grundmenge eines Wahrscheinlichkeitsraums und seien A, B, C Ω Ereignisse. Drücken Sie die Die Existenz allgemeiner diskreter Wahrscheinlichkeitsräume wird durch den großen Umordnungssatz für Reihen garantiert. Wichtige unendliche Reihen, die bei diskreten Verteilungen zum Tragen kommen, sind die Exponentialreihe, die

Ereignis Definition 1.2. Sei (Ω, Pr) ein diskreter Wahrscheinlichkeitsraum. Eine Menge A Ω heißt Ereignis. Die Wahrscheinlichkeit Pr [A] des Ereignisses A ist definiert als In der Wahrscheinlichkeitsrechnung und Statistik unterscheiden wir zwischen verschiedenen Arten von Verteilungen, die beschreiben, wie Wahrscheinlichkeiten auf verschiedene Ereignisse verteilt sind. Die zwei Hauptkategorien sind diskrete und stetige Verteilungen. In diesem Abschnitt konzentrieren wir uns auf stetige Verteilungen und deren grundlegende Eigenschaften sowie Die Funktion P nennt man gleichwertig auch eine Wahrscheinlichkeitsverteilung auf Ω. Weiter heißt jede Teilmenge E von Ω ein Ereignis. Jedem Ereignis E ordnen wir seine Wahrscheinlichkeit P (E) bzgl. (Ω, P) zu vermöge

DWT ©Ernst W. Mayr 1 Grundlagen 16/467 Ē heißt komplementäres Ereignis zu E. Allgemein verwenden wir bei der Definition von Ereignissen alle bekannten Operatoren aus der Mengenlehre. Wenn also A und B Ereignisse sind, dann sind auch A Die diskrete Wahrscheinlichkeitsrechnung bezieht sich auf abzählbare Ereignisse. Sie ist die Grundlage für die Wahrscheinlichkeitsrechnung. Mit der Mengenlehre werden Wahrscheinlichkeitsoperationen festgelegt. Die Kolmogorovschen Axiome fassen Regeln zur Berechnung von Wahrscheinlichkeiten zusammen. Der Begriff der Wahrscheinlichkeit bleibt Ausgangspunkt der Wahrscheinlichkeitstheorie sind Ereignisse, die als Mengen aufgefasst werden und denen Wahrscheinlichkeiten zugeordnet sind; Wahrscheinlichkeiten sind reelle Zahlen zwischen 0 und 1; die Zuordnung von Wahrscheinlichkeiten zu Ereignissen muss gewissen Mindestanforderungen genügen.

Viele Probleme in der Wahrscheinlichkeitsrechnung können gelöst werden mit Hilfe des Symmetrieprinzips, also mit Laplace-Wahrscheinlichkeiten. Das Berechnen der Wahrscheinlichkeiten bedeutet dann das Zählen von Ergebnissen. Es ist klar, dass die Theorie des Zählens, die Kombinatorik, dabei ein wichtiges Hilfsmittel ist. In diesem Kapitel Wahrscheinlichkeitsräum 1 e 1.1. Diskret Wahrscheinlichkeitsräume e 2 1.2. Allgemein Wahrscheinlichkeitsräume e 12 1.3. Existenzproblem cr-Algebre: 2n 0 1.4. Existenzproblem Wahrscheinlichkeitsmaß: 3e 2 1.5. Bedingt Wahrscheinlichkeitee 4n 0 Aufgaben 42 Kapitel 2. Zufall variable 4s 5 2.1. Meßbar Abbildungee n und Zufallsvariabl 4e 5 2.2.

M1.1 Diskrete Strukturen (1. Teil des Moduls M1: Mathematik für die Informatik 1) – Detailseite Funktionen: Seiteninhalt: Grunddaten Termine Zugeordnete Person Studiengänge Einrichtungen Inhalt Strukturbaum Remove ads Wahrscheinlichkeitstheorie • • • Axiomatischer Aufbau Definitionen Axiome von Kolmogorow Folgerungen Abzählbare Ergebnismenge Überabzählbare Ergebnismenge Spezielle Eigenschaften im Fall diskreter Wahrscheinlichkeitsräume Laplace-Experimente Bedingte Wahrscheinlichkeit Verbundwahrscheinlichkeit (Schnittmengen von Ereignissen) Satz von

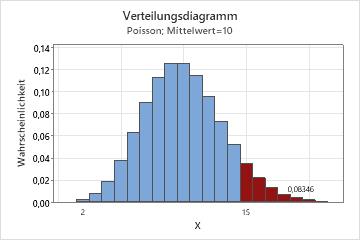
1.1 Einfuhrung und Motivation Wahrscheinlichkeiten werden im taglichen Sprachgebrauch verwendet und intuitiv verstanden. Hieraus entwickeln wir dann in mehreren Schritten das gangige Konzept der Wahrscheinlichkeits-theorie, die Axiomatik von Kolmogoro . Eine diskrete Zufallsvariable X ist Poisson-verteilt mit Parameter λ falls X die #Ereignisse in einem festen Interval mit Rate λ modelliert, wobei die Ereignisse unabhängig von der Zeit seit dem letzten Ereignis auftreten.

Inhalt: Diskrete Wahrscheinlichkeitsräume, bedingte Wahrscheinlichkeiten, Unabhängigkeit, Zufallsgrößen, Gesetze der großen Zahlen, Große Abweichungen, die eindimensionale Irrfahrt, Poisson- und Normalapproximation der Bionomialverteilung, allgemeine Wahrscheinlichkeitsräume und Zufallsgrößen mit Dichten, rekurrente Ereignisse Vorbemerkungen Das Material zu diesem Skript habe ich im Wesentlichen dem Buch von Georgii (2007) sowie Vorlesungsskripten von Gerhard Osius entnommen. Sollten sich in den übernommenen Teilen Fehler finden, so bin dafür natürlich ich verantwortlich. Lob und positive Kritik gebührt indes den Original-Autoren.

QQCWB

GV