QQCWB

GV

Einstein And Debye Models _ Einstein Model vs Debye model.

Di: Ava

The Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat (heat capacity) in a solid. This This article emphasizes that the Einstein and Debye models of specific heats of solids are correlated more tightly than currently acknowledged. This correlation is evi-denced without need of

Specific Heat Capacity | PPTX | Chemistry | Science

Chapter 2: Problem 8 Einstein versus Debye* In both the Einstein model and the Debye model the high-temperature heat capacity is of the form C = N k B (1 κ / T 2 + ). For the Einstein model calculate κ in terms of the Einstein temperature. For the Debye model calculate κ in terms of the Debye temperature.

The Einstein model describes each atom in a solid as an independent quantum harmonic oscillator with the same eigenfrequency ω 0. Using the Debye solid In 1912, Peter Debye generalised Einstein’s model of a solid. The Debye solid has improved low temperature behaviour, namely, a heat capacity oc T!. Debye related the oscillations of atoms to sound waves propagating through the solid. We investigated an amorphous Ni 46 Ti 54 alloy produced by mechanical alloying using extended x-ray absorption fine structure (EXAFS) technique and cumulant expansion considering Einstein and Debye models for the temperature dependence of the cumulants. Results obtained from both models were compared and very similar values were obtained.

The Oxford Solid State Basics Solutions to Exercises

Hier sollte eine Beschreibung angezeigt werden, diese Seite lässt dies jedoch nicht zu. 3.2. Debye’s modification to Einstein’s model of specific heat Debye did a major improvement of the Einstein’s model. He treated the coupled vibrations of the solid in terms of 3 N normal modes of vibration of the entire solid, each with its own frequency.

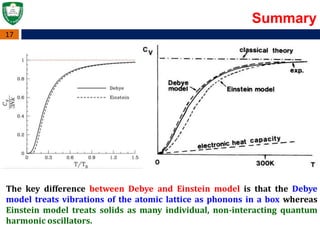
The reason for the failure of the Einstein model in the low T limit is that the model does not allow for low-frequency modes, which are of dominant importance at low temperatures. The Debye model is much more successful in this respect and correctly predicts the form of the specific heat at low temperatures.

The Einstein solid is a model of a crystalline solid that contains a large number of independent three-dimensional quantum harmonic oscillators of the same frequency. The independence assumption is relaxed in the Debye model. While the model provides qualitative agreement with experimental data, especially for the high-temperature limit, these oscillations are in fact The document discusses the Einstein and Debye models of heat capacity in solids. The Einstein model from 1907 treats each atom as an independent harmonic oscillator vibrating at the same frequency. In contrast, the Debye model from 1912 treats the solid as a continuous elastic body with a range of vibration frequencies, improving on Einstein’s assumptions. Both models aim to Abstract This article emphasizes that the Einstein and Debye models of specific heats of solids are correlated more tightly than currently acknowledged. This correlation is evidenced without need of additional hypotheses on the early Einstein model. The results are also extensible to the case of a system of fermions; as an example, the specific heat of the electron sea in metals is

  • Debye Model — Statistical Physics Notes
  • DEBYE THEORY OF SPECIFIC HEAT SOLVED PROBLEMS
  • Debye Model For Specific Heat

Debye model The key simplification of the Einstein model is to consider the atoms as independent quantum harmonic oscillators. Instead of independent oscillators, Peter Debye considered the collective motion of atoms as sound waves. Sound waves A sound wave is a collective motion of atoms through a solid.

The agreement between values of results obtained from this model and the experimental data is very good, as shown in Figure 73, as those Debye results compared to both Einstein and Dulong-Petit results. What is Debye model theory? In solid-state physics, debye theory is used to estimate the phonons contributing to the specific heat capacity in a solid. It explains that the specific heat is a consequence of the vibrations of the atomic lattice of the solid, which is in contrast to the Einstein model. In the Einstein model, solids are treated as independent, non-interacting quantum

The Debye model treats atomic vibrations as phonons in a box, while the Einstein model considers each atom in the solid lattice as an independent 3D quantum harmonic oscillator. The Debye model accurately explains the low-temperature dependence of heat capacity, proportional to T^3, and recovers the Dulong-Petit law at high temperatures. In contrast, the

Einstein Model vs Debye model.

The correlated Einstein and Debye models for EXAFS parallel mean-square relative displacement (MSRD) are derived from the general expression in terms of eigenfrequencies and eigenvectors of the dynamical matrix, without ad hoc assumptions. The two models are generalized to parameterize also the EXAFS perpendicular MSRD. Chap 13 Phonons classical theory of vibration 1-dim, 3-dim quantum theory of vibration phonon specific heat Einstein model, Debye model thermal expansion neutron scattering

Important We start for the Einstein’s theory and reaches a ‘non-sleeping’ model. What happened when we integrated over all DoS in Debye model? This is because our density of states \ (g (\omega)\propto \omega^2\) at low temperature tells us that we would have more states at a certain energy as \ (\omega\) increases. Planck’s suggestion4,5. Both the Dulong-Petit and Einstein models assume independent atomic vibration. Born and Von Karman6 proposed that the bonding in solid phase prevents independent atomic vibration and that the vibration should be collective lattice oscillation. If the particles are interacting then The Debye model assumes a contribution of acoustic phonons with omega (k) ~ k, where the number of modes is determined by the cut-off frequency omega_Debye (or, expressed as a temperature, k_B theta_Debye = hbar omega_Debye). The Einstein model assumes that the phonon energy hbar omega_Einstein is independent of the wave vector k.

The Debye–Einstein model An approach based on the Debye–Einstein heat capacity model has been used to analyse the revealed regularities, which has proved itself well for low-temperature studies of the heat capacity of substances in various classes [19–26]. Solid State Physics problem set covering Einstein, Debye, Drude, and Free Electron Models. Includes chemical bonding and phonon topics. ASSUMPTIONS OF DEBYE MODEL The vibration of the crystal as a whole is considered equivalent to the vibrational motion of a system of coupled harmonic oscillator.

Hier sollte eine Beschreibung angezeigt werden, diese Seite lässt dies jedoch nicht zu. In this video, specific heat of solids have been plotted at different temperatures using three different models (Dulong Petit, Einstein and Debye). Plotting

The Debye Einstein model is also an effective method to predict the thermal properties of multicomponent materials. In Debye Einstein model, the 3n−3 optical frequencies at the Γ point are considered to represent the contribution of the optical branches, which significantly reduces the computational cost compared with QHA. The document provides solutions to various exercises related to the specific heat of solids, discussing classical and quantum mechanical treatments, including calculations of classical partition functions and heat capacities for both Einstein and Debye models. It further examines concepts of Fermi energy and surface in metals, deriving expressions related to free electron • Use Bose-Einstein statistics to determine the number of phonons in each mode Specific Heat of Solid 8 Approximate Models: The Debye Model Replace exact phonon dispersion relation and the density of modes with the density of modes of an elastic continuum, but include a cut-off frequency, the Debye frequency ωD X Γ X ωD Determination of ωD

Debye Model — Statistical Physics Notes

1) The document discusses quantum mechanical models of heat conduction in solids, specifically the Einstein and Debye models. 2) The Einstein model treats the solid as independent harmonic oscillators all with the same frequency. This crude model gives the correct high temperature limit but fails at low temperatures. 3) The Debye model accounts for the actual distribution of

Einstein and Debye Models for Specific Heat Prof Dr Hasan Sahin

In thermodynamics and solid state physics, the Debye model is a method developed by Peter Debye in 1912 [1] for estimating the phonon contribution to the specific heat (heat capacity) in a solid. It treats the vibrations of the atomic lattice (heat) as phonons in a box, in contrast to Einstein model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. In the Einstein model, atoms are treated as independent oscillators. The Debye model on the other hand, treats atoms as coupled oscillators vibrating collectively. However, the collective modes are regarded here as independent. What is the meaning of this independence and how does it contrast

Lecture notes on the Einstein model and the Debye model.

The Debye model, developed by Peter Debye in 1912, refined Einstein’s model by considering the collective nature of atomic vibrations. Debye’s model recognized that atoms in a solid are not independent entities but rather interact with each other, giving rise to collective vibrational modes known as phonons. Ans. The Einstein theory of specific heat is a quantum mechanical model proposed by Albert Einstein to explain the behavior of specific heat in solids.

Brillouin Zones and their importance:

This makes the Debye Model more accurate for predicting heat capacity at lower temperatures, as it incorporates the complexity of atomic interactions while still addressing vibrational behavior. Evaluate the significance of the Einstein Model in solid-state physics and its influence on later models like the Debye Model.

T of highly mobile conduction electrons is approximated by Einstein Model, which is composed of single-frequency quantum harmonic oscillators. The temperature dependence of Einstein model is just T. It becomes significant at low temperatures and is combined with the above lattice specific heat in the Einstein-Debye specific heat [3] .