QQCWB

GV

Delphi Hilfe Bei Der Hilbert Kurve

Di: Ava

Die Hilbert-Kurve, oder genauer der Hilbert-Polygonzug, ist ein Beispiel für eine flächenfüllende Kurve und ein Beispiel dafür, dass der Dimensionsbegriff neu überdacht werden muss. Thema / Inhalt Hier geht es um Rekursion, im engeren Sinne um rekursives Problemlösen – also der Einsatz von Rekursion als Technik, um in algorithmischer Weise ein Berechnungsproblem zu lösen. Wir betrachten zunächst einige Kurven (u.a. die Peano-Kurve und die Hilbert-Kurve), die entsprechend eines rekursiven Bildungsgesetzes aufgebaut sind und einen intuitiven Zugang

Vielleicht haben Sie bemerkt, dass es in unserer neuen Version von PrusaSlicer (2.3) neue Infill-Muster gibt. Nun, bei der schieren Menge an Optionen fühlen Sie sich vielleicht sogar überwältigt von all den Möglichkeiten. Welches Infill sollten Sie wählen? Gibt es ein Hallo zusammen, ich habe eine TChart-Komponente, der ich zur Laufzeit mehrere TFastLineSeries hinzufüge. Jede dieser LineSeries stellt eine Kurve da, Delphi-PRAXiS (https://www.delphipraxis.net/forum.php) – GUI-Design mit VCL / FireMonkey / Common Controls (https://www.delphipraxis.net/18-gui-design-mit-vcl-firemonkey-common-controls/)

Kann mir jemand dir Hilbert Kurve einfach erklären?

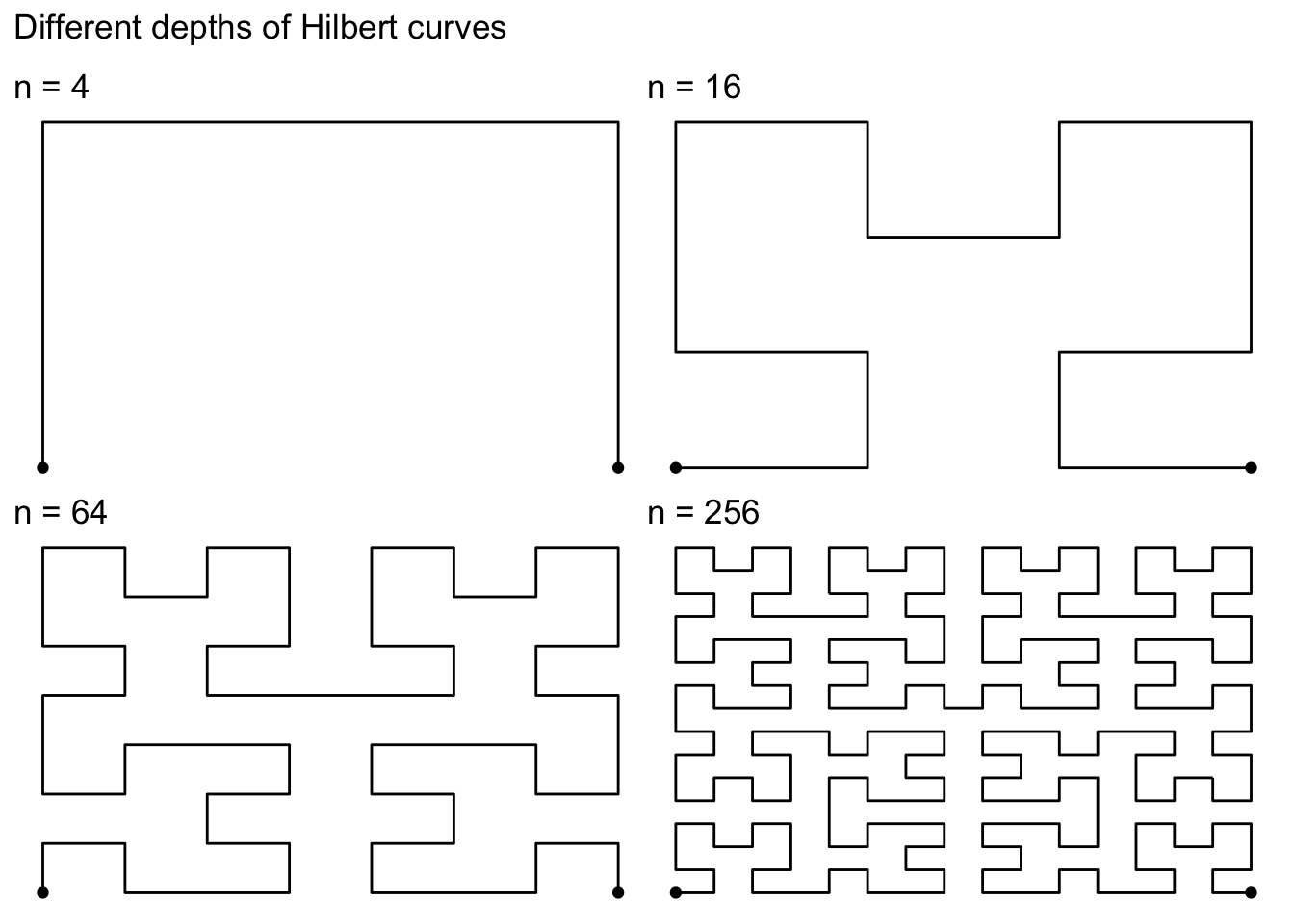
A Fast ggplot2-Based Implementation of Hilbert Curves • gghilbertstrings

Die Hilbert-Kurve als Beispiel für eine flächenfüllende Kurve Weitz / HAW Hamburg 62.1K subscribers Subscribed In einer Zeit, in der das 20. Jahrhundert noch in den Kinderschuhen steckte und die Welt rasante wissenschaftliche und technologische Fortschritte erlebte, erstrahlte David Hilbert als ein imposantes Leuchtfeuer im Reich der Mathematik. Nicht nur als Sprachrohr und Vordenker einer ganzen Disziplin, sondern auch durch seine eigenen unbestreitbaren, Die Hilbert-Kurve besteht aus nur einer zusammenhängenden „Linie“, die mit jedem Rekursionsschritt mehr und mehr Raum einnimmt. Daher nennt man die

Delphi (griechisch Δελφοί (m. pl.), altgriechisch ΔελφοίDelphoí ausgesprochen), ursprünglich Pytho (Πυθώ) genannt, war eine Stadt im antiken Griechenland, die vor allem für ihr Orakel bekannt war. Seit 1987 gehören die Ausgrabungen von

Normalerweise funktioniert der Code also. Nur eben in bestimmten Fällen nicht Tritt eine Exception auf, so erscheint, wenn das Programm in der IDE läuft folgende Meldung: Delphi 1-7: ab Delphi 8: Auch hier landet man mit einem kurzen Tastendruck auf [F1] an der entsprechenden Stelle in der Hilfe und erfährt, was es mit der Exception auf Home » Object Pascal » Objekte erzeugen und freigeben Objekte erzeugen und freigeben Objekte erzeugen: Der Konstruktor Eigener Konstruktor Objekte freigeben: Der Destruktor Eigener Destruktor Objekte erzeugen: Der Konstruktor Instanzen einer Klasse entstehen erst dadurch, dass sie ausdrücklich erzeugt werden. Dies geschieht mit dem Konstruktor Create. Eine Hilbert-Kurve (nach D. Hilbert) ist eine Linie, die eine Fläche beliebig dicht ausfüllt, je nach Anzahl der Iterationen. Wir beschreiben im Folgenden eine Hilbert-Kurve durch ein L-System, dessen Zeichen als Turtle-Grafik-Operationen interpretiert werden.

Die Hilbert-Kurve ist eine besondere mathematische Struktur, die 1908 von David Hilbert erstmals beschrieben wurde Die Hilbert-Kurve besteht aus nur einer zusammenhängenden „Linie“, die mit jedem Rekursionsschritt mehr und mehr Raum einnimmt. Eine dreidimensionale Version der Hilbert-Kurve gibt es hier als 3D-Druck. Hallo, ich brauche dringend hilfe. Ich soll einen Taschenrechner bauen bei dem ich unendlich zahlen eingeben kann. Er soll addieren, Subtrahieren, „Das Buch soll dazu dienen, die Freude an der Mathematik zu mehren, indem es dem Leser erleichtert, in das Wesen der Mathematik einzudringen, ohne sich einem beschwerlichen Studium zu unterziehen“ (David Hilbert, Anschauliche Geometrie, 1932)

Generator, der fraktale Kurven und Pflanzen generiert

  • Die Hilbert-Kurve als Beispiel für eine flächenfüllende Kurve
  • dict.cc Deutsch-Englisch-Wörterbuch
  • Lindenmayer-Systeme: Raumfüllende Kurven

Um 1903 führte Hilbert, bei der Untersuchung eines Problems von Integralgleichungen, den unendlichdimensionalen euklidischen Raum ein, der heute nach ihm benannt wird. zu den Hilbert-Kurven zum Hilbert Hotel | Delphi-PRAXiS (https://www.delphipraxis.net/forum.php) – GUI-Design mit VCL / FireMonkey / Common Controls (https://www.delphipraxis.net/18-gui-design-mit-vcl-firemonkey-common-controls/) Die Hilbert-Kurve ist eine vom deutschen Mathematiker David Hilbert (1862-1943) gegen Ende des 19. Jahrhunders entdeckte raumfüllende Kurve in einer Einheitsfläche. Das bedeutet, dass sie keine eindimensionale Kurve darin darstellt, sondern die komplette Fläche. Für die Konstruktion wird in jedem Schritt ein Teilintervall und das entsprechende Quadrat in vier Teile aufgeteilt.

Das dürften allerdings keine großen Hindernisse sein. Eine Übersicht über die Versionsnummern von HTML-Hilfe und Internet Explorer sowie aktuelle Entwicklungen finden Sie unter HTML-Help Tech Info der Helpware Group. Delphi-Units Da Delphi wie gesagt, die chm-Hilfe nicht direkt unterstützt, werden entsprechende Units benötigt.

Problem wurde im Jahr 2000 von dem Mathematikhistoriker Rüdiger Thiele von der Universität Leipzig in Hilberts Nachlass entdeckt. Es beschäftigt sich mit Beweistheorie, einem Teilgebiet der mathematischen Logik, bei der mathematische Sätze und vor allem ihre Beweise selbst Gegenstand der Forschung sind, siehe unten. Zum 130.

Beschreibung gluNurbsProperty wird benutzt um die Eigenschaften des NURBS-Objekts zu steuern. Diese Eigenschaften beeinflussen die Art und Weise wie die NURBS-Kurve gerendert wird. Gültige Werte für property sind folgende: GLU_SAMPLING_TOLERANCE Gibt die maximale Länge in Pixeln an, die benutzt werden soll, wenn die Samplingmethode auf Die Hilbert-Kurve ist eine vom deutschen Mathematiker David Hilbert (1862-1943) gegen Ende des 19. Jahrhunders entdeckte raumfüllende Kurve in einer Einheitsfläche. Das bedeutet, dass sie keine eindimensionale Kurve darin darstellt, sondern die komplette Fläche. Für die Konstruktion wird in jedem Schritt ein Teilintervall und das entsprechende Quadrat in vier Teile aufgeteilt.

Egal, ob du Schwierigkeiten mit Dynamik und Bewegung, Hilberträumen, Kurven und Flächen hast, ich bin hier, um dir persönliche Unterstützung zu günstigen Preisen mit unbegrenzten Überarbeitungen für deine Zufriedenheit zu bieten. Die Entwickler-Ecke ist eine Community für Entwickler. Unser Fokus liegt auf .NET / C#, Delphi und Web (JavaScript, PHP, HTML, CSS). Wir sind aber offen für Fragen zu allen Sprachen / Plattformen.

Wer mit RAD Studio, Delphi oder C++Builder arbeitet, weiß: Der Einstieg ist einfach – doch manchmal braucht man Hilfe. Ob es um eine Lizenzübertragung, ein Registrierungsproblem oder eine technische Frage zur IDE geht – viele Kunden fragen uns: „Wo bekomme ich Support?“ oder „Wie greife ich auf meine Downloads zu?“ Die gute Nachricht: Anwendungen der Hilbert-Transformation Manfred Zollner Die Hilbert-Transformation ist eine Abbildung aus der Systemtheorie. Ihre häufigste Anwendung findet sie bei der Umformung eines reellen Signals in ein analytisches, sie stellt bei minimal-phasigen Systemen aber auch eine Beziehung zwischen Betrag und Phase her. Die höherdimensionalen Hilbert-Kurven sind eine Verallgemeinerung von Gray-Codes , die aus denselben Gründen für ähnliche Zwecke verwendet werden. Für mehrdimensionale Datenbanken haben wir die Verwendung der Hilbert-Ordnung anstelle der Z-Ordnung vorgeschlagen, da sie sich beim Erhalten der Position besser verhält.

Schau dir unsere Auswahl an hilbert kurve an, um die tollsten einzigartigen oder spezialgefertigten, handgemachten Stücke aus unseren Shops zu finden. Fraktal-Generator Einführung Helge Koch, Cesare Peano und David Hilbert schufen die erste fraktalen Kurven als ‚Monster‘ zur Analysis. Die Koch-Kurve Hallo, In meinem Delphi Tokyo 10.2.2 ist die Hilfedatei defekt. Wie kann ich die Hilfedatei ersetzen ohne das Programm neu zu installieren ??? Für

11.1 Die Hilbert-Kurve Von David Hilbert, einem der bedeutendsten deutschen Mathematiker, stammt die Idee zu einer besonderen „Kurve“, die heute nach ihm benannt ist: Nach einer festen Regel wird von Schritt zu Schritt eine Strecke „verformt“ – je nach Lage der Strecke auf unterschiedliche Weise. Ein Blick auf motivische Hilbert-Zeta-Funktionen und ihre Rolle beim Studieren von Kurven. In der Welt der Mathematik gibt’s jede Menge faszinierender Hallo Leute, ich habe in meinem Javapraktikum die Aufgabe mit MVC die Peano und die Hilbertkurve zu zeichen. Die beiden Kurven sollen per Rekursion berechnet werden. Die Hilbertkurve habe ich schon hinbekommen: [code=Java] /* orient = Drehrichtuung +1 oder

11.1 Die Hilbert-Kurve Von David Hilbert, einem der bedeutendsten deutschen Mathematiker, stammt die Idee zu einer besonderen „Kurve“, die heute nach ihm benannt ist: Nach einer festen Regel wird von Schritt zu Schritt eine Strecke „verformt“ – je nach Lage der Strecke auf unterschiedliche Weise. David Hilbert (1912) David Hilbert (* 23. Januar 1862 in Königsberg; [1] † 14. Februar 1943 in Göttingen) war ein deutscher Mathematiker und Hochschullehrer. Er gilt als einer der bedeutendsten Mathematiker der Neuzeit, [2] den Rudolf Fueter 1932 den „Lehrer aller lebenden Mathematiker“ nannte. [3] Viele seiner Arbeiten auf den verschiedenen Teilgebieten der Fragen zum Aufbau von Programmen mittels Algorithmen, Strukturen und Klassendesign

– Sonstige Fragen zu Delphi (https://www.delphipraxis.net/19-sonstige-fragen-zu-delphi/) – – DelphiDarstellung einer Kurve in Delphi (https://www.delphipraxis.net/109478-darstellung-einer-kurve-delphi.html)

Hilbert-Kurven sind nach ihrem Erfinder D.Hilbert (1891) benannt. Sie entstehen, wenn vier Einheiten (die einem Quadrat mit einer fehlenden Seite