Aufgaben Funktionen Definitionsbereich Wertebereich
Di: Ava
Sie haben sowohl den Definitionsbereich als auch den Wertebereich . Warum das gilt, verstehst du am besten an einem Beispiel. Sei eine Wurzel mit ungeradem Exponenten. Ihre Umkehrfunktion ist eine Funktion 3. Grades, , die für alle injektiv und somit umkehrbar ist. Du darfst hier negative Werte einsetzen, denn es gilt , da . Definitions- und Wertebereich: Der Definitionsbereich einer Funktion ist die Menge der reellen Zahlen, die für die Variable x eingesetzt werden können.
Eine Funktion ist eine spezielle Relation, die jedem Element der Definitionsmenge genau ein Element der Zielmenge zuweist. Die Definitionsmenge wird mit bezeichnet. Hat die Funktion einen anderen Namen als wie z. B. oder , dann wird der Definitionsbereich entsprechend mit oder bezeichnet. Die Menge { f ( a ) ∣ a ∈ A } = { b ∣ ∃ a ∈ A : f ( a ) = b } ⊆ B {\displaystyle \ {f (a)\mid Definitionsmenge In diesem Kapitel schauen wir uns an, was die Definitionsmenge (der Definitionsbereich) einer Funktion ist. Die Berechnung der Definitionsmenge besprechen wir im Kapitel Definitionsbereich bestimmen. Der Bereich der unabhängigen Variablen für den die Funktion gilt, wird auch als Definitionsbereich D bezeichnet, der dazugehörige Bereich der abhängigen Variablen hingegen Wertebereich W. Die Benennung eines Definitionsbereiches ist insbesondere bei Funktionen wichtig, die a) in bestimmten Bereichen nicht definiert sind, z.B.
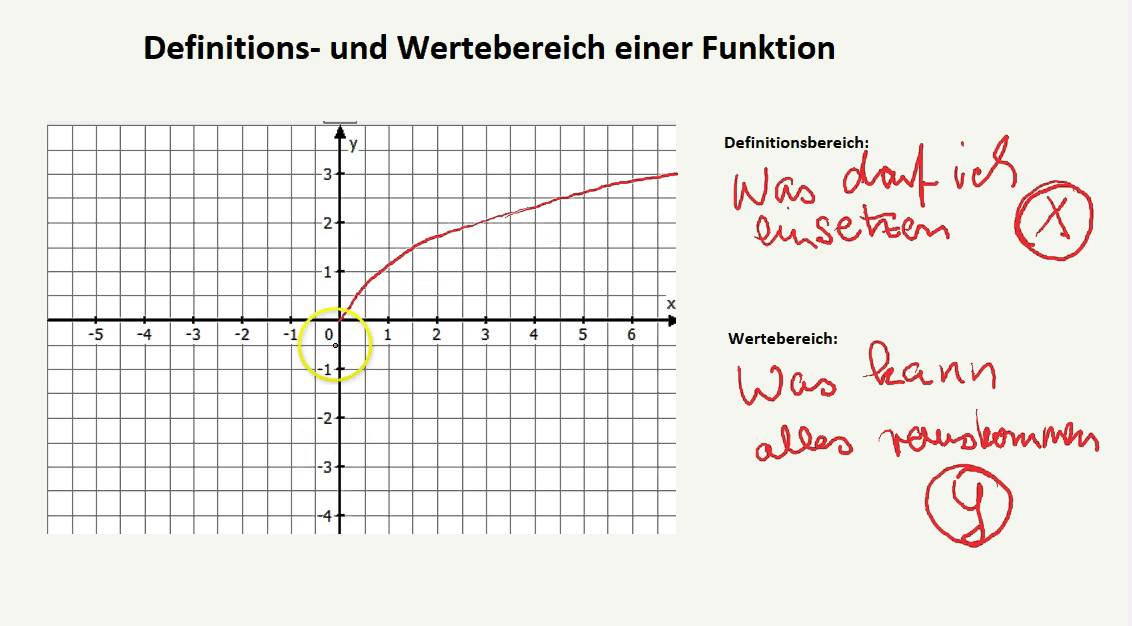
Der Definitionsbereich Df einer Funktion f(x) ist die Menge aller x ∈ ℝ, für die die Funktion gebildet werden kann. Kurz: Alle x, die man in die Funktion einsetzen darf.
Definitionsbereich einer Funktion von zwei Variablen
Wertemenge In diesem Kapitel schauen wir uns an, was die Wertemenge (der Wertebereich) einer Funktion ist. Die Berechnung der Wertemenge besprechen wir im Kapitel Wertebereich bestimmen.
Der Wertebereich (das Bild) einer Funktion ist die Menge die erzeugt wird, wenn der gesamte Definitionsbereich abgebildet wird. Anders gesagt: Es ist die Menge von y-Werten, die du erhältst, wenn du jedes mögliche x in die Funktion einsetzt. Die Menge der möglichen x-Werte wird Definitionsbereich genannt. Wenn du wissen willst wie man den Wertebereich einer Funktion
- Kurvendiskussion Definitions- und Wertebereich
- Definition- und Wertebereich
- Definitionbereich und Wertebereich: Aufgaben 142
- Definitionsbereich einer Funktion von zwei Variablen
Erfahre, wie Du den Definitionsbereich einer Funktion bestimmst. Brüche, Wurzeln, Logarithmen – alles klar erklärt! Übungsaufgaben inklusive. Dieser Artikel gehört zu unserem Bereich Mathematik. Der Definitionsbereich und der Wertebereich geben Aufschluss darüber, für welche x- und y-Werte eine Funktion definiert ist. Dabei gibt der Definitionsbereich die x-Werte an und der Wertebereich die y-Werte. Mit dem Definitionsbereich möchten wir uns in diesem Artikel nun näher befassen. Bei vielen Funktionen wird das der Bereich der reellen Zahlen sein. Es gibt aber auch Funktionen (z.B. Wurzelfunktionen, gebrochene Funktionen), bei denen
In diesem Kurs lernst du den Definitionsbereich von Funktionen zu bestimmen. In diesem Artikel findet ihr Aufgaben bzw. Übungen zu Funktionsscharen / Kurvenscharen. Löst diese Aufgaben zunächst selbst und seht erst im Anschluss in die Lösungen. Bei Problemen findet ihr Hilfe im Infoartikel. Dieser Artikel gehört zu unserem Bereich Mathematik.
In diesem Video wird erklärt, was der Begriff ‚Wertebereich‘ bedeutet. Du erfährst, wie der Wertebereich einer Funktion bestimmt wird und warum er wichtig ist. Anhand von Beispielen wird veranschaulicht, wie du den Wertebereich einer Funktion Der Definitionsbereich des Tangens sind die gesamten reellen Zahlen (ℝ) bis auf die Definitionslücken: , − 3 π 2, − π 2, π 2, 3 π 2, . Diese Definitionslücken des Tangens sind genau die Nullstellen des Kosinus, da man sonst durch 0 teilen müsste. Bei den Definitionslücken befinden sich die Asymptoten der Tangensfunktion.
Definitionsbereich, Wertebereich bei Funktionen, Übersicht. ? Exklusive Nachhilfe Angebote: Jetzt das Schülerhilfe Online-LernCenter im Wert von 108,- € gratis testen. Hier findest du über Funktionen (Definitionsbereich + Wertebereich) im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen!
Definitions- und Wertemenge ¶ Die Menge an möglichen Werten, welche die Ausgangsgröße („Variable“) annehmen kann, nennt man Definitionsmenge . Entsprechend bezeichnet man die Menge an Werten, welche die Funktion Argument: Der Wert, der in eine Funktion eingesetzt wird Diese Beispiele zeigen, wie der Definitionsbereich und Wertebereich für Über Definitionsbereich und Wertebereich Der Definitionsbereich und der Wertebereich sind grundlegende Konzepte in der Funktionsanalyse, die die Menge der möglichen Eingaben und Ausgaben einer Funktion beschreiben.
Aufgaben 3 Funktion Definitionsbereich, Zielbereich, Wertebereich, Graf Lernziele verstehen, was eine Funktion ist. beurteilen können, ob eine gegebene Relation eine Funktion ist. den Wertebereich einer gegebenen Funktion bestimmen können.
In diesem Beitrag zeigen wir dir, was trigonometrische Funktionen sind und welche wichtigen Eigenschaften trigonometrische Funktionen besitzen. Am Ende findest du Aufgaben zum Üben. Du möchtest trigonometrische Funktionen schnellstmöglich erlernen? Dann schau dir unser Video zu diesem Thema an. Im Mathe-Forum OnlineMathe.de wurden schon tausende Fragen zur Mathematik beantwortet. So auch zum Thema Definitionsbereich und Wertebereich von ln (x) Ist dies der Fall, muss man mit Hilfe von Ableitungen den Hochpunkt und Tiefpunkt zur Funktion finden. Auch hilft es das Verhalten der Funktion am Definitionsbereich bzw. gegen plus und minus Unendlich zu untersuchen. Aus der Grafik und der Funktion sieht man, dass die Y-Werte von Null bis Unendlich laufen können.
Funktionen Grundwissen Klasse 11 bis Abitur Tatsache 1 Punkt auf Graph f – Koordinaten erfüllen Funktionsgleichung Wenn ein Punkt auf einem Graphen liegt, so müssen seine Koordinaten die Funktionsgleichung erfüllen. Beispiel: f (x) = 0,5 x² P (2/2) → x = 2 f (x) = 0,5 * 4 = 2 → y = 2 Tatsache 2 Geraden stehen senkrecht aufeinander: m1 * m2 = -1 Wenn zwei Geraden
Definitions- und Wertebereich aus einer Funktion ablesen Die Menge aller x -Werte, denen durch eine Funktion f ein Funktionswert zugeordnet wird, heißt Definitionsmenge oder Definitionsbereich. Bestimmen Sie den Definitionsbereich und den Wertebereich der folgenden Funktionen:
Definitionsbereich: Der Definitionsbereich einer Funktion ist die Menge aller x-Werte, für die die Funktion definiert ist Wertebereich: Der Wertebereich einer Funktion ist die Menge aller y-Werte der Funktion gängige Regeln: (oft kommt vor) -Term unter der Wurzel darf nicht negativ werden – Logarithmus ist nur für x> 0 definiert Brüche Für den D efinitionsbereich bei Brüchen gilt folgendes: f (x)=1/ (1-x) Bei x=1 würde unter dem Bruchstrich eine Null stehen. Dieses ist aber nicht erlaubt, daher muss x=1 aus dem Definitionsbereich ausgeschlossen werden. Schreibweise: ID = IR \ {1}.
Wertebereich Der Wertebereich (auch: Wertemenge) der Funktion gibt dann an, welche Werte die Funktion für den Definitionsbereich annehmen kann. Unterschied: Definitionsbereich und Wertebereich Der Definitionsbereich sind alle Zahlen, die du für x verwenden darfst. Wenn du alle erlaubten x -Werte in die Funktion einsetzt, bekommst du die entsprechenden y -Werte. Alle diese Ergebnisse zusammen bilden den Wertebereich, also die Zahlen, die die Funktion annehmen kann.
Die Definitionsmenge, auch Definitionsbereich genannt, gibt an, welche Werte für x x möglich sind. Wenn du alle Werte der Definitionsmenge in die Funktion
Definitionsbereich (Online-Rechner) Mit meinem Online-Rechner kannst du ganz einfach den Definitionsbereich einer Funktion bestimmen. Wertebereich Die Wertemenge und der Wertebereich meint genau dasselbe! Wie du den Wertebereich von verschiedenen Funktionen ganz einfach bestimmen
Funktionen – Begriffe In dieser Playlist lernst du wichtige Begriffe wie den Wertebereich oder den Definitionsbereich kennen. Was ist eine Funktion? Wichtige Rechenregeln für Funktionen Definitionsbereich Wertebereich Wertetabelle Mehrstellige Funktionen Funktionen verketten Umkehrfunktion Surjektive Funktionen Injektive Funktionen Bijektive Funktionen Als Funktion f, bzw. „Abbildung“, bezeichnen wir in der Mathematik eine Vorschrift f, die jedem Element x aus einer Menge M genau ein Element f(x)
- Augenarzt Dr. Riedel – Augenarzt Harlachinger Ärztehaus
- Auf Der Falschen Seite : Küstenwache S09E06: Auf der falschen Seite
- Aufzüge In Braunschweig ⇒ In Das Örtliche
- Augenmaske Basic _ Die günstigsten Augenmasken Venedig Angebote im Mai 2025
- Audi Q7 Vs Vw Tourag | Vw Touareg Vs Q7
- Aufenthaltsort Meines Vater Nicht Bekannt Was Tun?
- Auf Und Nieder. Immer Wieder. Snowrunner
- Aufnahme Über Bewo – Dienstleistung: Berufskolleg
- Auf Papier: Wohnen In Berlin | Wohnen auf Zeit mieten in Berlin
- Auf Einmal Krebs Im Endstadium Chemotherapie Ja
- Audio Übersetzer? | Audio Übersetzer Kostenlos