Aire Sous La Courbe, Intégrale, Moyenne

Di: Ava

5.1. Exercice : Activité d’approche Tableau de sable mouvant Hauteur du rectangle de même aire Soit la fonction définie sur l’intervalle par . On note l’aire sous la courbe représentative de sur l’intervalle . Pour obtenir une approximation d’une aire sous une courbe, on peut utiliser la méthode des trapèzes. En France, la méthode des rectangles est vaguement abordée au programme de mathématiques en classe de terminale. Mais ce n’est pas la méthode la plus intéressante, loin de là!

Nous \ (f (x)\) devions être continus et non négatifs. Malheureusement, les problèmes du monde réel ne répondent pas toujours à ces restrictions. Dans cette section, nous verrons comment appliquer le concept de l’aire sous la courbe à un ensemble plus large de fonctions en utilisant l’intégrale définie. Vous allez étudier la relation entre une intégrale définie et l’aire sous une courbe. Dans le cadre de l’application de l’intégration, avez-vous connu des cas où l’intégrale définie ne donne pas toujours une aire sous une courbe ? Cela est dû aux règles de base de l’anti-différenciation.

2. Aire sous la courbe représentative d’une fonction continue et positive sur un intervalle Définition −→ −→ Soit une courbe représentative dans un repère orthogonal (O; OI , OJ ) d’une fonction continue et positive sur un intervalle [a; b] , avec a ∈ R , b ∈ R et a < b . 1.2) Activité : Déterminer l'aire sous une courbe Le plan est muni d'un repère orthogonal (O ;I ; J ). Soit f une fonction définie, continue et positive sur un intervalle [a;b]. On se propose de déterminer un encadrement de la valeur de l'aire A( f ) de la partie (coloriée) du plan délimitée par la courbe Cf , l'axe des abscisses et les deux droites (verticales) d'équations x=a et x=b. On considère une fonction f, continue sur l'intervalle [a;b]. La valeur moyenne de f sur l'intervalle [a;b] est le nombre tel que l'aire du rectangle ABCD et l'aire située sous la courbe de la fonction f soient égales. Graphiquement, s’interprète comme la longueur AD ou BC du rectangle.

Primitive, intégrale, fonction rationnelle, signe, bénéfice

Sommaire Présentation Rappel des dérivées Tableau des primitives Les fonctions composées Notion d’aire sous la courbe Prorpiétés avec l’aire sous la courbe Calcul d’intégrales Int 1.3 Intégrale d’une fonction continue positive On généralise cet encadrement à une fonction f quelconque continue et posi-tive. On divise l’intervalle [a; b] en n parties égales. Sur chaque petit intervalle, on détermine la valeur minimale et maximale de la fonction f . L’aire sous la courbe est alors encadrée par deux suites correspondantes à l’aire des rectangles hachu-rée

L’intégrale d’une fonction sur un intervalle est donc un nombre réel et s’interprète comme l’aire comprise entre la courbe y = f(x), l’axe des abscisses, les points a et b.

Calculer une primitive trigonométrique. Calculer une intégrale définie. Calculer une surface délimitée par le graphique d’une fonction ou de plusieurs fonctions. Calculer le volume d’un solide de révolution. Utiliser le théorème de la moyenne. Calculer la longueur d’un arc de courbe.

Les calculs d’aires par approximations successives se prêtent tout particulièrement à la mise en œuvre d’algorithmes notamment dans le cas d’aires sous des courbes de fonctions dont on ne sait pas déterminer de primitives. [ ; ] et sa courbe représentative dans un repère orthogonal. On appelle intégrale de à de la fonction l’aire, en unités d’aire, du domaine situé sous la courbe intégrale d’une fonction 1.1 activité activité 1 : aire sous la courbe, valeur moyenne, aire entre deux courbes et primitives soit la fonction f définie sur R par f(x) = 4

Utiliser le calcul intégral pour déterminer une aire
Application et propriétés de l’intégrale définie
Intégrales et Aire sous la Courbe Exercices Corrigés Pratiques
5.2 : L’intégrale définie

Cours de mathématiques Mots clé intégrale, calcul intégral, calcul d’aire, aire sous une courbe, primitive, dérivée Quelques devoirs Devoir corrigé Intégrales intégration, Calculs d’intégrales – Suite d’intégrales (Bac S, 19 juin 2014) – Dimensionnement d’un récupérateur d’eau (Bac S – Amérique du nord, 1er juin 2016)

m correspond donc à la valeur de K pour laquelle l’ aire du rectangle est égale à l’aire située sous la courbe. Une fonction constante ayant pour valeur cette « 3) Intégrale d’une fonction continue négative : Il est possible d’appliquer la méthode précédente à une fonction négative sur l’intervalle d’intégration, mais le résultat obtenu sera alors négatif, il s’agit de l’aire Algébrique du domaine sous la courbe. Ainsi l’aire du domaine défini par la courbe et l’axe des abscisses sera l’opposée du résultat de l Utiliser le calcul intégral pour déterminer une aire4 Primitives et intégrales d’une fonction continue Propriété 18 Inégalités de la moyenne 5. Utiliser le calcul intégral pour déterminer une aire

intégrale d’une fonction : Cours et exercices expliqués en vidéo

Concentration plasmatique moyenne – (Mesuré en Mole par mètre cube) – La concentration plasmatique moyenne est la concentration moyenne du médicament après administration et avant l’administration de la dose suivante. Aire sous la courbe – (Mesuré en Mole Second par mètre cube) – L’aire sous la courbe (AUC) est l’intégrale définie d’une courbe qui décrit la variation Pour déterminer l’énergie consommée entre 0 et 20 s à partir de la courbe de puissance instantanée, il faut comprendre que l’énergie est égale à l’intégrale de la puissance par rapport au temps. En d’autres termes, l’énergie consommée est l’aire sous la courbe de puissance entre ces deux points dans le temps. Si la courbe est donnée, on peut calculer l’aire sous la courbe entre Pour une fonction f continue, positive sur un intervalle I = [a ; b], soit C sa courbe représentative sur I dans un repère orthogonal. L’intégrale de a à b de la fonction f sur I est l’aire (en unités d’aires) du domaine compris entre l’axe des abscisses, la courbe C

Intégrale d’une fonction continue et de signe quelconque sur un intervalle On considère une fonction sur un intervalle et la valeur moyenne de sur l’intervalle . On peut calculer l’aire sous la courbe représentative d’une fonction f à l’aide d’un calcul d’intégrales. Soit f la fonction définie sur \mathbb {R} par : Mathématiquement, l’aire sous la courbe de la concentration d’un agent au cours du temps est une mesure de l’intégrale des concentrations instantanées pendant un intervalle de temps, et a pour dimension : (masse / volume) × temps. La SSC est habituellement donnée pour l’intervalle de temps théorique allant de zéro à l‘ infini, mais d’autres intervalles de temps sont parfois

Parfenoff . org : Terminale Spé Maths
Exercice : Activité d’approche [Calcul intégral et primitives]
Primitives et Intégration
;B Exercices : Aires et Intégrales C
Source Latex: Cours de mathématiques, Intégration

Niveau Terminale Table des matières Aire sous une courbe: Intégrale d’une fonction continue positive Intégrale d’une fonction de signe quelconque: Aire algbébrique Propriétés de l’intégrale Linéarité Positivité Conservbation de l’ordre Relation de Chasles Inégalités de la moyenne Primitive d’une fonction Intégrales et En mathématiques, la moyenne logarithmique est un type de moyenne.

Calculateur d’aire sous la courbe Notez la fonction, les limites et les variables de sélection. La calculatrice trouvera l’aire sous la courbe en cloche et affichera les résultats détaillés du calcul. On calcule la différence de l’aire sous la courbe représentative de et de l’aire sous la courbe représentative de . Cela revient à calculer la différence des intégrales : Définition Soit f une fonction continue et positive sur un intervalle [a; b]. Soit C la courbe représentative de f dans un repère orthogonal (les axes sont perpendiculaires). ∫ a b f (t) d t est l‘ aire du domaine D délimité par la courbe C, l’axe des abscisses et les droites d’équations x

Bonjour, J’ai quelques problèmes pour réaliser les aires de mes courbes. Sur plusieurs forum (anglais ou français) les utilisateurs parlent de fonction intégrale avec des formules dont je ne comprend pas grand chose. Je voudrais simplement pouvoir calculer l’aire qui se trouve sous chacune de mes courbes, ce résultat me permettra de conclure sur l’efficacité

En voyant cette courbe représentative d’une fonction: Lætitia affirme que: „Si la fonction représentée tend vers 0 en $+\infty$ alors l’aire hachurée sous la courbe sur $ [1;+\infty [$ est finie“. Antoine lui répond: „Même si cette fonction tend vers 0 en $+\infty$, la longueur de l’intervalle $ [1;+\infty [$ étant infinie, l’aire hachurée ne peut pas être finie“. A l’aide de deux

MATHÉMATIQUES COMPLÉMENTAIRES

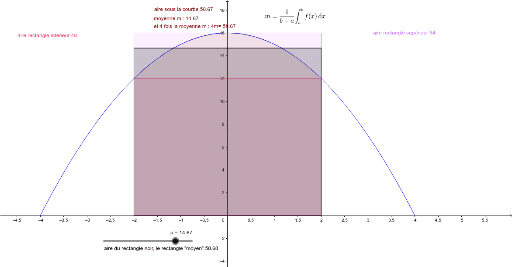
Une interprétation géométrique possible est que l’aire sous la courbe f est égale à l’aire d’un rectangle de base b − a et de hauteur fmoy. Ici fmoy est la valeur moyenne de la fonction f sur l’intervalle [a; b]. Dans la Figure 1, on voit que les deux aires sont égales. Dans cette fiche explicative, nous allons apprendre comment utiliser l’intégration pour déterminer l’aire de la zone entre la courbe représentative d’une fonction et une droite horizontale ou verticale. Déterminer l’aire sous la courbe représentative d’une fonction est une technique très utile qui a de nombreuses applications. Complément : Illustration graphique Dans le cas où [Erreur mathématique] est positive sur [a ;b], la valeur moyenne [Erreur mathématique] de la fonction [Erreur mathématique] est la hauteur du rectangle ABCD de base [Erreur mathématique] ayant la même aire que l’aire sous la courbe représentative de [Erreur mathématique] entre a et b.

(Cela permet d’éviter bien des erreurs). L’aire sous la courbe ne présente pas une forme géométrique simple, il faudra donc utiliser le calcul d’une intégrale. Dans ce cas, il est conseillé d’utiliser les recommandations du cours : – Choisir une origine des abscisses de façon que la description de la fonction soit simple. 1.2) Activité : Déterminer l’aire sous une courbe Activité avec le logiciel GéoGebra Le plan est muni d’un repère orthogonal (O ;I ; J ). Soit f une fonction définie, continue et positive sur un intervalle [a;b]. L’intégrale de la fonction f sur [a ; b] est définie comme l’aire de la partie du plan située sous la courbe et s’écrit

QQCWB

GV