3E Tangente D’Un Angle Aigu Dans Un Triangle Rectangle
Di: Ava
Quels sont les rapports trigonométriques? Les rapports trigonométriques dans un triangle rectangle sont le cosinus, le sinus, la tangente, la sécante, la cosécante et la cotangente. Ces rapports permettent de déterminer des mesures manquantes ou des angles manquants dans un triangle rectangle.
Calculer le sinus, le cosinus et la tangente d’un angle Définition 1 : Vocabulaire du triangle rectangle Propriété : cohérence de la définition de cosinus, sinus et tangente Dans un triangle rectangle, on décide de regarder l’un des deux angles aigus. Les rapports . : côté adjacent . côté opposé hypoténuse hypoténuse . côté opposé côté adjacent ne dépendent par de la « taille » du triangle rectangle considéré mais seulement de la mesure en degré de l’angle aigu qui est
approchée du cosinus d u
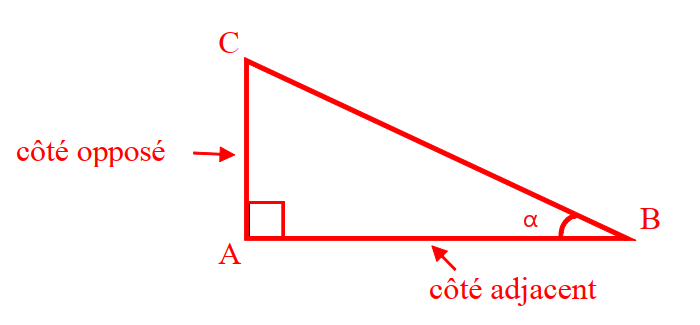
Dans le triangle ABC rectangle en C, les rapports de longueurs ABCA, ABCB et CACB ne dépendent que de la mesure de l’angle BAC. Ainsi, on appelle : le cosinus d’un angle aigu le quotient égal à : longueur de l’hypoteˊnuse longueur du coˆteˊ adjacent a l’angle ; le sinus d’un angle aigu le quotient égal à : longueur de l’hypoteˊnuse longueur du coteˊ opposeˊ l’angle ; la Connaître et utiliser dans le triangle rectangle des relations entre le cosinus, le sinus ou la tangente d’un angle aigu et les longueurs de 2 côtés du triangle. I / Introduction Le mot trigonométrievient du grec et signifie « mesure du triangle ». Le cosinus, le sinus et la tangente sont trois rapports trigonométriques. ⇒ feuille d’activités II / Définitions 1°) • Étant donné un triangle ABC rectangle en B, considérons l’un
Fonctions sinus, cosinus et tangente dans le cadre du triangle rectangle. Relations entre les fonctions trigonométriques. Conversion entre degrés et radians. – Q1: Dans un triangle rectangle, quel côté est toujours opposé à l’angle droit ? L’hypoténuse, Le côté adjacent, Le côté opposé,
Relations trigonométriques dans le triangle rectangle Objectifs : – déterminer une valeur du sinus, du cosinus ou de la tangente d’un angle En raison de limitations techniques, la typographie souhaitable du titre, « Trigonométrie : Tangente dans un triangle rectangle Trigonométrie/Tangente dans un triangle rectangle », n’a pu être restituée correctement ci-dessus. En conclusion, pour trouver la mesure d’un angle aigu dans un triangle rectangle, nous pouvons utiliser les rapports trigonométriques tels que le sinus, le cosinus et la tangente. En utilisant les mesures des côtés du triangle, nous pouvons résoudre ces équations et trouver les mesures des angles aigus.
- RAPPORTS TRIGONOMÉTRIQUES
- Trigonométrie dans le triangle rectangle
- Trigonométrie 3ème : ce qu’il faut savoir pour le brevet
Cours de maths complet sur la trigonométrie en 3ème. Définitions, applications, calcul de longueurs, calcul de la mesure d’un angle, exercice et vidéos sur Mathforu. Exercice 1: ? ? ? est un triangle rectangle en ?. 1) On considère l’angle aigu ? : LA TRIGONOMÉTRIE : SINUS, COSINUS, TANGENTE Bienvenue dans le monde fascinant de la trigonométrie ! Aujourd’hui, on va explorer trois notions essentielles : le sinus, le cosinus et la tangente. Ces outils sont super utiles pour résoudre des problèmes liés aux triangles rectangles. Prêt (e) ? C’est parti ! 1. LES BASES : LE TRIANGLE RECTANGLE Avant de
Si on connaît deux côtés d’un triangle rectangle, on peut calculer la mesure des trois angles. 3.Rapports trigonométriques d’un angle aigu et relations métriques dans un triangle rectangle – Free download as PDF File (.pdf), Text File (.txt) or read Page 1. « Comment calculer un angle aigu dans un triangle rectangle ? » Il faut connaître : – la longueur de deux côtés du triangle. PDF 3e Tangente dun angle aigu dans un triangle rectangle Dans un triangle rectangle : il faut savoir reconnaître : Le côté adjacent à un angle aigu le côté opposé à un angle aigu et l’hypoténuse de ce triangle PDF
Trigonométrie dans un triangle rectangle I) Cosinus, sinus et tangente d’un angle aigu dans un triangle rectangle 1) Vocabulaire : Dans un triangle rectangle : il faut savoir reconnaître : Le côté adjacent à un angle aigu, le côté opposé à un angle aigu et l’hypoténuse de ce triangle rectangle : 1er cas possible : 2ème cas Série 3 : Synthèse Le cours avec les aides animées Q1. Dans quelle configuration peut-on appliquer la trigonométrie ? Q2. Donne la définition du cosinus, du sinus et de la tangente d’un angle aigu dans un triangle rectangle.

Dans un triangle rectangle : Côté opposé O Le sinus d’un angle aigu est le quotient : S = Hypoténuse H Côté adjacent A Le cosinus d’un angle aigu est le quotient : C = Dans un triangle A B C rectangle en A, on définit le cosinus, le sinus et la tangente de l’angle aigu A B C ^ de la manière suivante : cos A B C ^ = côté
- Math: comment calculer les angles dans un triangle rectangle
- Relations trigonométriques dans un triangle rectangle 3e
- Trigonométrie : l’essentiel en 3ème
- Tangente: qu’est-ce que c’est, comment la calculer, exemples
2. Définition du cosinus, du sinus et de la tangente d’un angle aigu d’un triangle rectangle ABC est un triangle rectangle en A. Un triangle rectangle est un triangle dans lequel un angle est droit, ce qui signifie qu’il est exactement 90 °. Pour ces triangles, il est possible de calculer les autres angles en utilisant des fonctions goniométriques comme le sinus, le cosinus et la tangente.
Nous définirons donc, dans un premier temps, ces rapports trigonométriques que sont les cosinus, sinus et tangente d’un angle aigu dans un triangle rectangle.
Exemple d’exercice corrigé pas à pas Énoncé : Dans un triangle rectangle, on connaît un angle aigu de 35° et la longueur de l’hypoténuse (10 cm). On cherche la longueur du côté adjacent à cet angle. Étape 1 : On identifie l’angle (35°) et on note que l’on connaît l’hypoténuse et que l’on cherche le côté I – Cosinus, sinus et tangente d’un angle aigu 1 – Définitions : Dans un triangle rectangle le sinus d’un angle aigu est le quotient de la longueur du côté opposé à cet angle par la longueur de l’hypoténuse.
La trigonométrie dans le triangle rectangle dans un cours de maths en 3ème avec le cosinus (cos), le sinus (sin) et la tangente (tan).
CHAPITRE 6 TRIGONOMETRIE DANS LE TRIANGLE RECTANGLE I – Cosinus, sinus et tangente d’un angle aigu : On considère le triangle ABC rectangle en A : B hypoténuse côté adjacent
I- Les rapports trigonométriques d’un angle aigu 1) Vocabulaire A B C est un triangle rectangle en A On considère l’angle A B C ^ Formules : Dans un triangle rectangle, on définit le sinus, le cosinus et la tangente d’un angle (différente de celui de l’angle droit) :
Vocabulary: L’hypoténuse est le côté le plus long du triangle rectangle, opposé à l’angle droit. Le chapitre se termine en mettant l’accent sur l’importance de comprendre ces relations pour maîtriser pleinement la trigonométrie dans le triangle rectangle et résoudre efficacement une variété de problèmes géométriques.
Calculer le cosinus, le sinus et la tangente d’un angle aigu dans un triangle rectangle. Calculer une longueur en utilisant la trigonométrie dans un triangle rectangle. Soit $ (\Delta)$ une droite donnée et $A$ un point du plan n’appartenant pas à $ (\Delta).$ Ce cours vous donnera des notions de trigonométrie: cosinus, sinus et tangente dans un triangle rectangle (à partir du niveau 3°). Tout d’abord, un petit rappel concernant le triangle rectangle : I. VocabulaireConsidérons un triangle rectangle : le plus grand côté est appelé hypoténuse du
La tangente d’un angle dans un triangle rectangle est définie comme le rapport entre la longueur du côté opposé à cet angle et la longueur de l’adjacent. On la note généralement par la lettre „tan“. Pour déterminer la tangente d’un angle, on peut utiliser différentes stratégies: calculer le rapport entre le sinus et le cosinus de l’angle, s’ils sont connus; utiliser une table tangente ou une calculatrice; calculer le rapport entre la jambe opposée et la jambe adjacente, si l’angle en question est interne (aigu) d’un triangle rectangle
̈ Définir sinus, cosinus et tangente d’un angle dans le triangle rectangle. ̈ Établir les nombres trigonométriques dans des triangles rectangles particu-liers (30°, 45° et 60°). ̈ Démontrer la formule fondamentale. ̈ Démontrer la relation entre les nombres trigonométriques. Dans un triangle rectangle, la tangente d’un angle est le rapport entre la mesure de la cathète opposée à l’angle et celle de la cathète adjacente. Trigonométrie dans le triangle rectangle 1) Les formules Les formules de trigonométrie permettent de calculer les longueurs des côtés dans un triangle rectangle, ainsi que la mesure des angles aigus.
- 3Er Regentonnen Netz Abdeckung
- 3D House Rendering _ Affordable 3D Rendering Services
- Leitungstrossen Protolon® Ntscgewöu/3E Von Faber
- 4 Bioenergetik Und Enzymologie
- 38 Fachanwälte Für Strafrecht In Hamburg
- 4 Best Music Marketing Ideas For Independent Artists
- 4 Nachnamen Zum Vornamen Avalon
- 3Er-Set Led-Sterne Für Feenhafte Außen-Beleuchtung
- 3500 Kg Autotransporter Ebay Kleinanzeigen Ist Jetzt Kleinanzeigen
- 360° Outdoor Wlan Überwachungskamera! Ip65 Kamera
- 360° Auto Kfz Halter Halterung Für Becker Revo.1
- 4 Soluciones Al Parpadeo De La Pantalla Del Iphone X
- 3D Lavender At Skyrim Special Edition Nexus
- 4 Of China’S Hottest Young Fashion Designers
- 3D Trasar 3Dt401 | SAFETY DATA SHEET 3D TRASAR 3DT408