1.Ableitung Von ^4, Was Kann Man Mit Hoch 4 Machen?
Di: Ava
Ableitungsrechner : Wie benutzt man es? Der Ableitung rechner online ermöglicht die Berechnung der Ableitung einer Funktion in Bezug auf eine Variable mit den Details und Berechnungsschritten. Syntax : ableitungsrechner (Funktion;Variable) Es ist auch möglich, die Leibniz-Notation mit dem Symbol `d/dx` zu verwenden. Beispiele : ableitungsrechner (sin Grafisches Ableiten und Aufleiten Anhand der folgenden Grafik kann man schön sehen, wie f (x), f ′ (x) und f “ (x) miteinander verbunden sind. Vielleicht kennt Graphisches Ableiten — häufigste Fragen Wie leite ich graphisch ab? Um einen Funktionsgraphen graphisch abzuleiten, untersuchst du wichtige Eigenschaften des Graphen, wie die Extrempunkte, Wendestellen und das Steigungsverhalten. Daraus kannst du den Ableitungsgraphen skizzieren. Was zeigt der Graph der ersten Ableitung? Mit der ersten
Ableitungsregeln einfach erklärt • Übersicht · [mit Video]
Negative Potenzen — Merke Bei Potenzen mit negativem Exponenten entsteht bei der Umformung ein Bruch. Im Zähler steht eine 1 und im Nenner steht die Basis hoch der Exponent mal – 1. Also die Basis mit dem positiven Exponenten. Mathe-lerntipps.de zeigt Ihnen ausführlich, wie Sie Extremwerte berechnen Berechnung von Hoch- und Tiefpunkten Mit Grafiken Mit Beispielen Jetzt kannst du dir als nächstes höhere Ableitungen von 1/x ansehen. Schau dir mal die zweite Ableitung an. Dafür musst du nochmal ableiten: Schritt 1 – Funktion umformen: Schreibe auch hier die Funktion zunächst ohne Bruch: f‘ (x) = -x -2 Schritt 2 – Funktion ableiten: Dann schiebst du den Exponenten wieder davor und ziehst vom Exponenten 1 ab: Schritt 3 – Funktion mit
![Ableitung mit Produktregel [Beispiele] - Einfach 1a erklärt](https://technikermathe.de/wp-content/uploads/2023/01/ma3-produktregel-beispiel.png)
Es kann sein, dass es mehrere Möglichkeiten gibt, ein Ableitung zu lösen. In diesem Fall werden die verschiedenen Lösungswege berechnet und ebenfalls angezeigt. Sollte der Rechner nicht in der Lage sein, den Rechenweg mit berechnen, wird die Software trotzdem versuchen, die Ableitung zu bestimmen. Ein Beispiel zu einer Kurvendiskussion wird ausführlich und Schritt für Schritt vorgerechnet und einfach erklärt. Dies wird für eine gebrochenrationale Funktion gezeigt und es wird von Nullstellen und Polstellen bis hin zu Ableitungen, Extrempunkten und mehr alles gründlich erläutert. Zum Seitenanfang Wir wissen, was der Anstieg einer Geraden ist – macht es auch Sinn, vom Anstieg einer Kurve zu sprechen? Wir wollen zunächst nicht allzu streng sein und uns von der Intuition leiten lassen: Eine Kurve kann ihre „Richtung“ ändern, sie kann in verschiedenen Punkten unterschiedlich „steil“ sein. Macht es also Sinn, von der Richtung und vom Anstieg
Ableitungsregeln Wie stark sich der Luftdruck ändert, wie schnell chemische Stoffe reagieren, wie viel Extra-Gewinn eine Firma machen kann: Die erste Ableitung \ (\displaystyle f‘ (x)\) hat viele anschauliche Bedeutungen. Um eine Funktion \ (\displaystyle f (x)\) nun ableiten zu können, benötigst Du Ableitungsregeln. Extremwerte berechnen In diesem Kapitel lernst du, wie man die Extremwerte einer Funktion berechnet. Graphisch betrachtet handelt es sich dabei um Hochpunkte bzw. Tiefpunkte.
Lerne die Ableitungsregeln richtig anzuwenden Kettenregel Potenz- & Faktorregel usw. kostenlose Übungsaufgaben.
Ableitungsrechner mit Rechenweg Online Rechner
Beispiel 1: Ableitung von ln x Beginnen wir mit der Ableitung der Funktion ln x. Deren Lösung entnimmt man einer Tabelle ( und benötigt noch keine Kettenregel ). Beispiel 2: Ableitung von ln 3x Um die Ableitung von ln 3x zu bestimmen, ist der Einsatz der Kettenregel nötig.
- Ableitungsregeln einfach erklärt • Übersicht · [mit Video]
- Dritte Ableitung einer Funktion
- Mit dem Taschenrechner Ableiten: Ein Leitfaden für Einsteiger
- Graphisches Ableiten • einfach erklärt · [mit Video]
Erfahre, wie man die Ableitung von Wurzelfunktionen wie Quadratwurzeln berechnet. Schritt-für-Schritt-Erklärung mit h-Methode. Einfache Ableitungsregeln. Alle Ableitungsregeln einfach erklärt Ableitung von Funktionen Anwendung der Ableitungsregeln mit Beispielen mit kostenlosem Video So kann man auch die Ableitung auf einen Graphen übertragen, die (1.) Ableitung einer Funktion bzw. eines Graphen ist deren Steigungsverhalten (also, wie verändert sich der Graph). Der Sinn von Ableitungen ist in der Regel nicht das
Ableitungsfunktionen und Ableitungen – Mathematik Erfahre, wie Ableitungen die Steigung und Krümmung von Funktionen beschreiben. Entdecke die Bedeutung von Ableitungen, Ableitungsregeln und wichtigen Ableitungsfunktionen. Inhaltsverzeichnis zum Thema Ableitungsfunktionen Ableitungsfunktionen im Überblick Ableitung und Ableitungsfunktion – Das Ableiten von Polynomen (oder ganzrationalen Funktionen) ist essentiell fürs Abi. Es wäre jammerschade und unnötig, wenn du da Fehler machen würdest. Darum hier ein paar Aufgaben zur Festigung. Dein Ziel sollte sein, dass du diese 1/4 Grundlagen des Ableitens Wie geht das Ableiten Der Prozess des Ableitens von Funktionen kann anfangs verwirrend sein, aber mit ein paar einfachen Regeln wird es viel einfacher. Eine dieser Regeln ist die Produktregel , die angewendet wird, wenn du eine Funktion hast, die aus der Multiplikation von zwei oder mehr Funktionen besteht. Eine andere wichtige
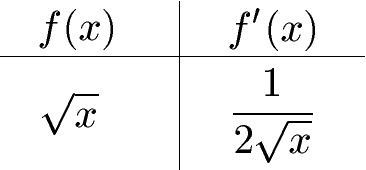
Dritte Ableitung einer Funktion verständlich erklärt vorgerechnete Aufgaben schneller Lernerfolg Klicken und lernen! Die 3. Ableitung einer Funktion an der Stelle x0 macht eine Aussage über den Wechsel des Krümmungsverhaltens vom Graph einer Funktion an der Stelle x0
Extremwerte berechnen ⇒ einfach & ausführlich erklärt
Mit der Ableitung einer Wurzel befassen wir uns in diesem Artikel. Dabei erklären wir euch, wie man Wurzel-Funktionen ableitet. Dieser Artikel gehört zu unserem Bereich Mathematik.
Schritt-für-Schritt-Ableitungsrechner online. Komplexe Funktionsregel, Addition, Multiplikation, Division und Modul. Mit Erklärungen! Auf dieser Seite erfährt man, wie man die Nullstellen, Extremstellen und Wendestellen (bzw. Nullpunkte, Extrempunkte und Wendepunkte) einer Funktion berechnet. Zudem wird gezeigt, welcher grafische Zusammenhang zwischen der Funktionsgleichung f (x), der 1. Ableitung f ´ (x) und der 2. Ableitung f “ (x) besteht. Auch weitere wichtige Elemente einer Kurvendiskussion Ableiten & Integrieren: Zusammenhang zwischen Weg, Geschwindigkeit, Beschleunigung und Ruck mit Diagrammen, Beispielen & Formeln erklärt.
Erfahre, wie die Ableitung einer Funktion ihre Steigung bestimmt, Extremstellen berechnet werden und Ableitungen in der Kurvendiskussion helfen. Mit dem Ableitungsrechner können Sie Ableitungen von mathematischen Formeln berechnen. Hierbei zeigt Ihnen der Ableitungsrechner sogar den Rechenweg. x 1 = 0,52752523 x 2 = -2,52752523 Artikel „Grafisches Ableiten“ aufrufen Zur Erinnerung: Die Nullstellen der abgeleiteten Funktion f‘ geben die x-Werte der Hoch- und Tiefpunkte der ursprünglichen Funktion wieder. Mit anderen Worten: An einem Hoch- oder Tiefpunkt von f hat die Ableitung f‘ eine Nullstelle.
Ableitung einer Funktion In einer Kurvendiskussion kannst du durch Ableiten insbesondere herausfinden, wo die Extrempunkte (Hoch- und Tiefpunkte ) einer Funktion liegen. Für unterschiedliche Funktionen brauchst du ganz unterschiedliche Regeln zum Ableiten. Die wichtigsten siehst du hier auf einen Blick: Was eine Ableitung in der Mathematik ist und wozu man diese brauch, lernt ihr hier. Dies sehen wir uns an: Eine Erklärung, was eine Ableitung ist. Beispiele als einfachen Einstieg zu Ableitungen. Aufgaben / Übungen um die Grundlagen zur Ableitung zu üben. Ein Video zu Ableitungen. Ein Frage- und Antwortbereich zu diesem Thema. Tipp: Wir sehen uns Nicht ganz. Das nennt man übrigens Integrieren 😉 Wenn f“ (x) = x^2, dann ist f‘ (x) = 1/3x^3 +c und f (x) = 1/12x^4 + cx + d c und d sind Konstanten, die man nicht bestimmen kann, weil sie die Kurve nur vertikal verschieben und auf die Steigung keinen Einfluss haben.
Ableitungen, Ableitung, ableiten, Ableitungsregeln
In diesem Video wird erklärt, wie man Ableitungen berechnet. Du lernst, was Ableitungen sind und wie du sie mithilfe von Regeln bestimmen kannst. Mit Beispielen und Schritt-für-Schritt Erklärungen wird dir gezeigt, wie du ableitest und wie du dabei vorgehst.
In diesem Artikel wird ausführlich erklärt, wie du die Ableitung von Variablen wie X bildest und welche Besonderheiten du dabei beachten musst. Weiter findest du hier eine Tabelle mit den wichtigsten Ableitungsregeln für bestimmte Terme sowie einen Online – Ableitungsrechner, mit dem du hier auf der Seite Terme direkt ableiten kannst. 1. Was sind Ableitungen
Funktionen dieser Art leitet man am einfachsten ab, indem man zuerst die funktionalen Brüche in eine negative Hochzahl umwandelt: f (x) = 1/x n = x -n Bei der Ableitung folgen Sie nun der ganz normalen Ableitungsregel, die Sie auch für Funktionen der Art f (x) = x n kennen. Ableitungen, Ableitung, ableiten, AbleitungsregelnA.13 | Ableitungen Was ist eine Ableitung überhaupt ? Die Ableitung einer Funktion f (x) gibt die Steigung bzw.
Ableitungsrechner Der Ableitungsrechner ermöglicht es Ihnen, die vom Benutzer eingegebenen Ableitungsfunktionen zu berechnen. Dies ist unter anderem bei der Untersuchung des Verlaufs der Funktionsvariabilität und der Bestimmung ihrer Extreme nützlich. Um eine Ableitung zu berechnen, geben Sie die Funktion in das untenstehende Feld ein.
Extremwerte, so genannte Hochpunkte und Tiefpunkte werden bei der Auswertung von Funktionen eingesetzt. Warum man dies überhaupt macht und wie es funktioniert, lernt ihr in diesem Artikel der Mathematik. Im nun folgenden gehen wir auf die Begriffe Extremwert, Hochpunkt und Tiefpunkt ein. Damit ihr diesen Artikel jedoch verstehen könnt, solltet ihr einige
Partielle Ableitungsrechner – Berechnen Sie partielle Ableitungen von mehrvariablen Funktionen und erhalten Sie detaillierte Schritt-für-Schritt-Lösungen! Was ist eine Kurvendiskussion? Bei einer Kurvendiskussion bestimmt man sämtliche charakteristischen Punkte einer Funktion, also Nullstellen, y-Achsenschnittpunkt, Hoch- und Tiefpunkte, Wendepunkt. Wie bestimmt man diese Punkte? Man bestimmt zuerst die erste, zweite und dritte Ableitung der Funktion.
- 10 Free Declaration Of Independence
- 10 Best Small Ice Cream Maker In 2024
- 10 Best Japanese Restaurants In Kl For Authentic Cuisines
- 10 Best Medicinal Plants In Mississippi
- 10 Best Motorhead Songs Of All Time
- 1.Fm Slow Jamz Webradio Live Hören Auf Phonostar.De
- 10 Best Snapchat Viewers: Watch Stories
- 1. Gang Beim M54 Geht Nicht | Leerlauf geht bei laufendem Moter nicht rein
- 1,5-Zimmer Wohnung Zur Miete In Borsigplatz
- 10 Best Esky Brands For Food And Drinks
- 10 Besten Elektriker In Springe, Region Hannover
- 1. Rheinisches Pionier-Bataillon Nr. 8
- 10 Best British Restaurants In Mayfair