QQCWB

GV

在直角三角形中:勾股定理A²＋B²＝C²是怎样证明而得到的？_百度知道

Di: Ava

In der Sprache der Mathematik: a² + b² = c² Diese Beziehung war schon lange vor Pythagoras bekannt, die alten Babylonier und Inder wendeten ihn in der Praxis an. Es gibt eine dreieinhalbtausend bis viertausend Jahre alte babylonische Keilschrift, auf der die Rechnung mit Beispielwerten beschrieben wird. ?分享鍛煉孩子思維和專註力的益智玩具?感謝您的關註#玩具 #益智玩具 #動手動腦 #燒腦遊戲 #解密遊戲 余弦定理是解三角形的重要结论之一. 它揭示的是三角形边角之间的关系. 是毕达哥拉斯定理的推广形式. 1.余弦定理的内容. 三角形任意一边的平方，等于另外两边的平方和减去这两边与它们夹角的余弦的积的2倍. 即：在 ABC中，设A、B、C对应的三边分别为a、b、c.则： a²=b²+c²-2bccosA. b²=a²+c²-2accosB

畢氏定理計算機：快速計算直角三角形邊長

勾股定理的公式有很多种，下面将介绍一些常见的勾股定理公式，希望对大家有所帮助。 1.直角三角形的勾股定理公式。 在直角三角形中，勾股定理可以表示为，a²+ b²= c²，其中a、b分别为直角三角形的两条直角边的长度，c为斜边的长度。 21 72 100 125 . . . Lösungen für Quadrupel mit a² + b² + c² = d² mit Tripel a² + b² = x² und b² + c² = y², a, b, c, d, x und y sind natürliche Zahlen. a b c d 264 448 975 1105 264 495 952 1105 357 1276 6960 7085 528 896 1950 2210 528 990 1904 2210 533 756 3360 3485 792 1344 2925 3315 792 1485 2856 3315 819 1680 3740 4181 861 5852 Use this law of cosines calculator to determine the third side of a triangle knowing two sides and the angle between them or to find the angles given all three sides.

在勾股定理的学习过程中，我们已经学会了运用如图图形，验证著名的勾股定理，这种根据图形直观推论或验证数学规律和公式的方法，简称为“无字证明 ...

正常三角形斜長的計算公式是：若一個三角形的三邊分別為a、b、c，則C-a-b=c。直角三角形可以運用勾股定理，c²＝a²+b²。勾股數組是滿足勾股定理a²+b²＝ c²的正整數組（a,b,c），其中的a,b,c稱為勾股數。例如（3,4,5）就是一組勾股數組。 三角形斜邊計算公式是什麼 1、勾股定理：c^2=a^2+b^2 2

If a+b+c =2, a²+b²+c² = 6, a³+b³+c³ = 8 then find the required result. MATHEMATICS IIT JEE 扫码下载作业帮 搜索答疑一搜即得

To solve for the hypotenuse, we simply take the square root of both sides of the equation a² + b² = c² and solve for c. When doing so, we get c = √ (a² + b²).

  • Teorema de Pitágoras: Fórmula e Exemplo
  • 勾股定理在线计算器,在线计算,在线计算器,计算器在线计算
  • 毕达哥拉斯定理——奇思妙想的证明方法

Was ist der Satz des Pythagoras? Satz des Pythagoras umstellen a² + b² = c² Schritt für Schritt erklärt mit kostenlosem Video 7、 三项完全平方公式：a²+b²+c²+2ab+2bc+2ac= (a+b+c)²。 8、 三项立方与公式：a³+b³+c³-3abc= (a+b+c) (a²+b²+c²-ab-bc-ac)。 三、 常见图形的面积公式 长方形的面积=长×宽S=ab 正方形的面积=边长×边长S=a² 三角形的面积=底×高÷2S=ah÷2 平行四边形的面

Teorema inverso do Teorema de Pitágoras

Calculations of geometric shapes and solids: Triangle.

余弦定理是一条重要的几何定理，其发展贯穿了古代数学的演进，涉及多个文明的贡献。最早关于余弦定理的思想可以追溯到古希腊数学家欧几里得的《几何原 Mathematik online und kostenlos erfolgreich lernen. Aufgaben Schritt für Schritt erklären mit Lösungen geeignet für Realschule Gymnasium Mittelschule 勾股定理, 直角三角形 的两条直角边的平方和等于斜边的平方. A²+B²=C² C=√（A²+B²） √（120²+90²）=√22500=√150²=150 例如直角三角形 的三条边是3（直角边）、4（直角边）、5（斜边） 3²+4²=5² 5=√（3²+4²）=√5²=5 扩展资料 勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和

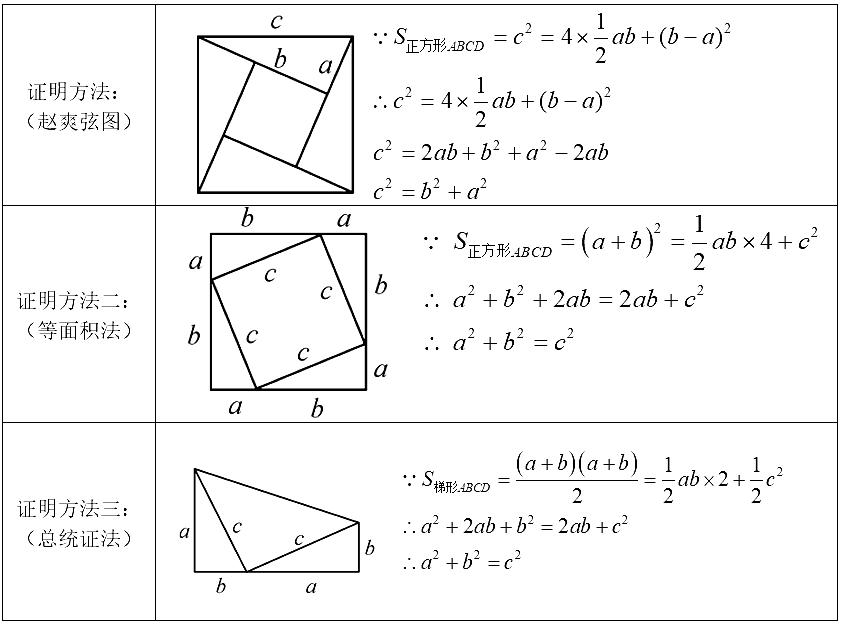
也就是说， 设直角三角形两直角边为a和b，斜边为c，那么a²+b²=c²。 勾股定理现发现约有400种证明方法，是数学定理中证明方法最多的定理之一。 赵爽在注解《周髀算经》中给出了“赵爽弦图”证明了勾股定理的准确性， 勾股数组程a² + b² = c²的正整数组 (a,b,c)。 Cours ♦ Théorème de Pythagore • Démonstration • Dans un triangle rectangle: a²+b²=c² ♦ Quatrième jaicompris Maths 433K subscribers Subscribed

Der wahrscheinlich bekannteste Lehrsatz der Geometrie bzw. Mathematik dürfte der Satz des Pythagoras sein: In einem rechtwinkligen Dreieck ist die Summe der Katheten-Quadrate gleich dem Quadrat der Hypotenuse. Den meisten Menschen dürfte der Satz des Pythagoras in Form der Gleichung a² + b² = c² geläufig sein, in dieser Form lässt er sich leicht merken. Erinnern wir uns zuerst an den Satz des Pythagoras mit a² + b² = c². Wenn wir die Hypotenuse mit c = 1 festlegen, dann ergibt sich bei Anwendung am Pour les triangles rectangles, les formules suivantes sont valables: t_2 a² + b² = c² (théorème de Pythagore) a² = c*p, b² = c*q (premier théorème d’Euclide) h² = p*q (théorème de la hauteur d’Euclide) sin alpha = a / c Triangle rectangle Qu’est-ce qu’un triangle rectangle? Un triangle rectangle est, comme son nom l’indique, un triangle contenant un angle droit, c’est-à-dire un

今天小编想和大家一起复习下初中几何定理的证明方法—— 毕达哥拉斯定理，是不是觉得没有印象，小编提起它的另一个名字你一定就想起来了，对，毕达哥拉斯定理也就是 勾股定理，公式为 a² + b² = c²。 勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一，各路大神奇思 Hier sollte eine Beschreibung angezeigt werden, diese Seite lässt dies jedoch nicht zu.

勾股定理公式大全表格-勾股定理公式大全表格如下：公式名称公式描述勾股定理基本公式a² + b² = c²在直角三角形中，直角边的平方和等于斜边的平方。 勾股定理求斜边公式c = √ (a² + b²)已知直角三角形的两条直角边a和b，求斜边c的长度。 柯西不等式公式分为二维柯西不等式的代数形式、柯西不等式的向量形式、三角不等式3个定理，具体的定理含义及基本题型 Mit diesem Rechner lassen sich wichtige Werte eines rechtwinkligen Dreiecks berechnen. Dafür werden der Satz des Pythagoras, der Kathetensatz des

O Teorema de Pitágoras diz que: o quadrado da medida da hipotenusa é equivalente a soma dos quadrados das medidas dos catetos. Entenda!

a²+b²+c²=ab+bc+ca a²+b²+c²-ab-bc-ac=0 2a²+2b²+2c²-2ab-2bc-2ac=0 (a²-2ab+b²)+ (b²-2bc+c²)+ (c²-2ac+a²)=0 (a-b)²+ (b-c)²+ (c-a)²=0 平方大于等于0,相加等于0,若有一个大于0,则至少有一个小于0,不成立. 所以三个都等于0 所以a-b=0,b-c=0,c-a=0 a=b,b=c,c=a 所以a=b=c 所以是等边三角形 畢氏定理（也稱為勾股定理）是一個關於直角三角形的重要數學定理。 它指出，在一個直角三角形中，直角對面的邊（斜邊）的平方等於其他兩邊的平方和。 這個定理可以用公式 a² + b² = c² 來表示，其中 c 是斜邊的長度，a 和 b 是另外兩邊的長度。 La suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, o sea a²=b²+c². Esto es lo que determina el teorema demostrado por Pitágoras (569 aC – 475 aC), matemático y filósofo griego.

Answer: The formula of a² + b² + c²= (a+b+c)²- (2ab + 2bc + 2ca) Step-by-step explanation: Concept: Recall the equation of (a+b+c)². Derivation for the formula a² + b² + c². Step1: we know the equation of (a+b+c)². Start from this equation. Step2: Subtract (2ab + 2bc + 2ca) from both sides Step 3: After subtraction we get Step 4: Rearranging the equation, we get

では、これはa²+b²=c²であることをどのように証明するのでしょうか。 青と緑の三角形の周りを移動するときは、それらの位置のみを移動します。

畢氏定理指出，在直角三角形中，斜邊（與直角相對的邊）的平方等於其他兩邊（腿）的平方和。 公式：a² + b² = c²，其中 c 是斜邊，a 和 b 是腿。 勾股定理是數學中描述直角三角形各邊關係的基本定理。 它指出斜邊（直角對邊）長度的平方等於其他兩條邊（腿）長度的平方和。 用數學術語來說，勾股定理可以表示為： a² + b² = c² 其中“a”和“b”是直角三角形兩條邊的長度，“c”是斜邊的長度。